SHARD: Spherical Harmonic-based Robust Outlier Detection for HARDI Methods
Citation: ” SHARD: Spherical Harmonic-based Robust Outlier Detection for HARDI Methods”. Vishwesh Nath, Ilwoo Lyu, Kurt G. Schilling, Allison E. Hainline, Prasanna Parvathaneni, Justin A. Blaber, Ilwoo Lyu, Adam W. Anderson, Hakmook Kang, Allen T. Newton, Baxter P. Rogers, Bennett A. Landman In SPIE Medical Imaging, International Society for Optics and Photonics, 2018 (Accepted)
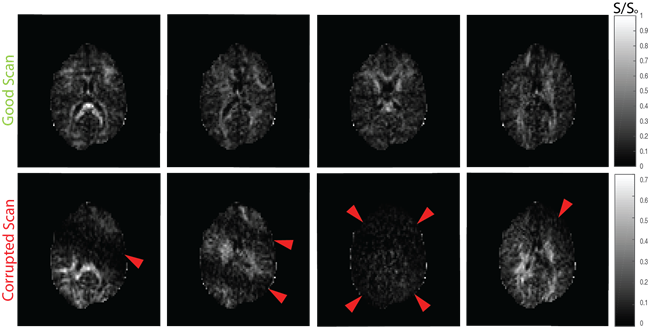
Abstract: High Angular Resolution Diffusion Imaging (HARDI) models are used to capture complex intra-voxel microarchitectures. The magnetic resonance imaging sequences that are sensitized to diffusion are often highly accelerated and prone to motion, physiologic, and imaging artifacts. In diffusion tensor imaging, robust statistical approaches have been shown to greatly reduce these adverse factors without human intervention. Similar approaches would be possible with HARDI methods, but robust versions of each distinct HARDI approach would be necessary. To avoid the computational and pragmatic burdens of creating individual robust HARDI analysis variants, we propose a robust outlier imputation model to mitigate outliers prior to traditional HARDI analysis. This model uses a weighted spherical harmonic fit of diffusion weighted magnetic resonance imaging scans to estimate the values which had been corrupted during acquisition to restore them. Briefly, spherical harmonics of 6th order were used to generate basis function which were weighted by diffusion signal for detection of outliers. For validation, a single healthy volunteer was scanned for a single session comprising of two scans one without head movement and the other with deliberate head movement at a b-value of 3000 s/mm2 with 64 diffusion weighted directions with a single b0 (5 averages) per scan. The deliberate motion from the volunteer created natural artifacts in the acquisition of one of the scans. The imputation model shows reduction in root mean squared error of the raw signal intensities and improvement for the HARDI method Q-ball in terms of the Angular Correlation Coefficient. The results reveal that there is quantitative and qualitative improvement. The proposed model can be used as general pre-processing model before implementing any HARDI model in general to restore the artifacts which are created because of the outlier diffusion signal in certain gradient volumes.