Research Sponsor:
U.S. Department of Energy (DoE), Nuclear Energy University Programs (NEUP) initiative.
Research Goal and Objectives
Goal:
Develop novel testing and experimentally validated prediction methodologies for creep-dominated creep fatigue response of Alloy 617.
Specific Objectives:
Formulate and implement models for the simulation of creep fatigue damage mechanisms and their interactions at the microstructure scale.
Conduct microstructure simulations to arrive at a better understanding of creep fatigue mechanism while developing a microstructure-informed and experimentally validated phenomenological life prediction framework.
Overview of Computational Tasks:
Formulation and implementation of a microstructure-based creep fatigue model.
- Develop CPFE model for Alloy 617 for modeling creep-fatigue deformation between 850°C and 950°C.
- Simulation-based mechanism understanding of CF interaction and life prediction through exercising the microstructure-based CF model.

Simulation-based mechanism understanding of CF interaction and life prediction through exercising the microstructure-based CF model.
Modeling Approach
Crystal Plasticity Theory:
Crystallographic slip driven by resolved shear stress are more favored than twin induced deformation for FCC metals.
Consider small elastic strain, arbitrary rotations and inelastic strains: applicable for most metals..
Formulation
Multiplicative decomposition of deformation gradient to and two intermediate configurations:
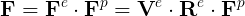
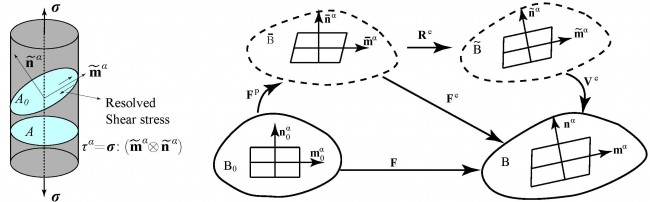
Velocity gradient in different configurations:

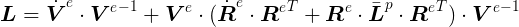
Decomposition of velocity gradients in different configurations:
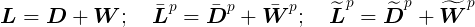
Choice of Flow Rule and Evolution Equations:
Solute drag creep phenomenon.
- Softening is observed at the tension part of first load cycle for both fatigue and creep-fatigue tests. Similar softening is also observed in the compression part after strain hold in each cycle of creep-fatigue tests.
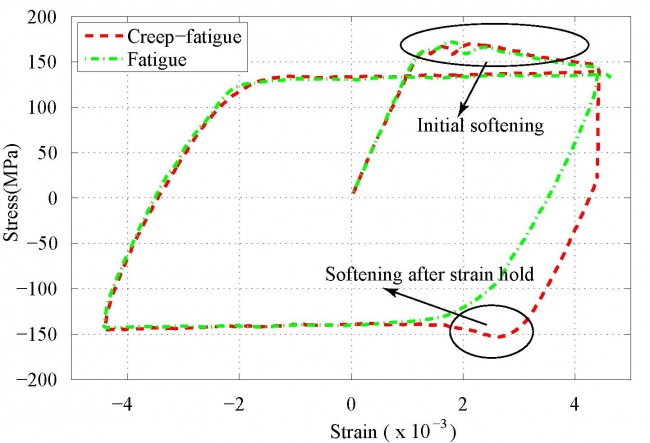
- Dislocation velocity increases with stress –> dislocation drag solutes hence extra resistance is produced –> dislocations accumulate enough energy to break solutes away from their equilibrium positions –> resistance drops as more and more solutes start moving together with dislocations.
- Strain hold –> dislocation velocity decreases with stress –> solutes settle down in new equilibrium positions –> softening happens when reverse loading is applied.
- In a fatigue tests, solutes do not have enough time to settle down in their new equilibrium positions as reverse loading follows immediately.
Flow rule and evolution equations to capture solute drag creep.
- Activation energy based flow rule for nickel-based alloy subject to cyclic loading at high temperatures (Busso[1996]):
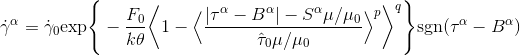
- Slip resistance evolution (Busso[2000]): from statistically stored forest obstacles.
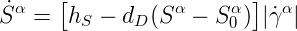
- Backstress evolution (Busso[1996]): from dislocations bowing between obstacles.
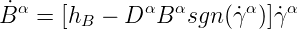
- New slip resistance evolution equation proposed by incorporating an static recovery which reflects the slip resistance changes caused by solute drag creep.
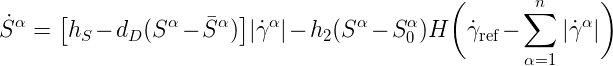
Modeling Preparation and Calibration
Microstructure reconstruction and meshing
Random initial orientation and bi-model grain size distribution from EBSD.
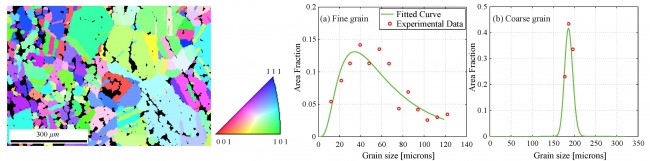
Synthetic microstructure reconstruction in DREAM.3D.
Surface mesh to volume mesh.
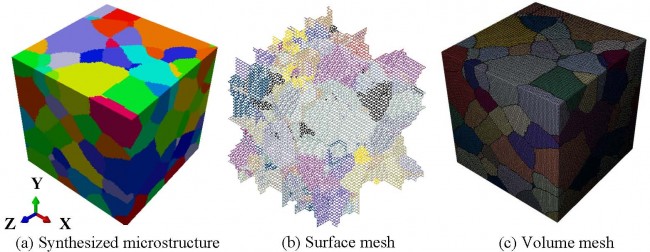
Mesh convergence study
Stress-strain and stress-time responses converge as grain size increases while computational costs increases.
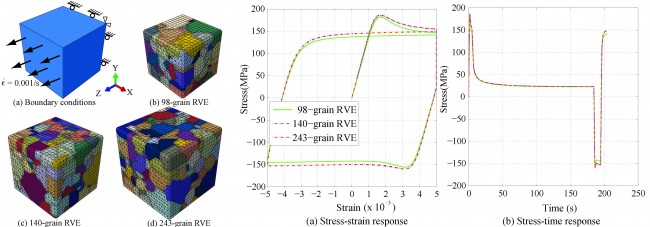
The 140-grain RVE is chosen for all simulations.
Model parameter calibration
A three stage (elastic, monotonic and hysteresis) calibration process is used to separately calibrate subsets of parameters.
A constrained nonlinear constrained optimization process minimizes the objective function:

A surrogate model based on Gaussian process to approximate the response during the second and third stages for efficiency.
Model Verification and Results Analysis
Stress-strain and stress-time response simulation.
Fatigue tests comparison:

Creep fatigue tests comparison:

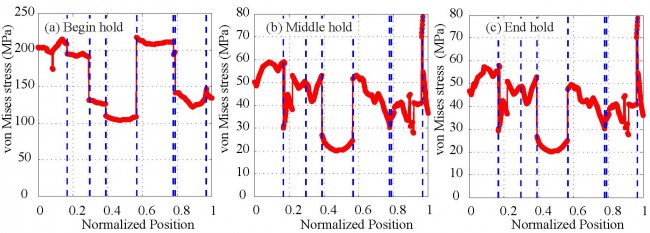
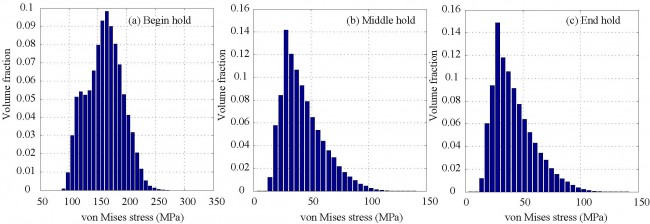
Analysis of CPFE Simulation Results.
Stress contour at different stages of the hold of the first cycle:

Stress distribution along a line passing the center of the RVE along X direction:
Histogram of von Mises stress at different stages of the first cycle:
Conclusion and Future Work
Conclusion
Current CPFE model takes the solute drag creep effect into account and well predicts the first cycle responses of fatigue and creep-fatigue tests with different strain range and hold time; It also provides a qualitatively prediction of the cyclic softening.
Future Work
Cohesive modeling of grain boundaries is ongoing and life prediction capability is expected ultimately.




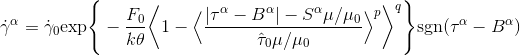
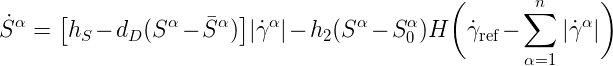









©2025 Vanderbilt University ·
Site Development: University Web Communications