Points on Spheres and Manifolds
(294) “Riesz Energy with a Radial External Field: When is the Equilibrium Support a Sphere?” (with Djalil Chafaï, Ryan W. Matzke, Minh Quan H. Vu, Robert S. Womersley), https://arxiv.org/abs/2405.00120
(293) On a problem of E. Meckes for the unitary eigenvalue process on an arc, (with Liudmyla Kryvonos), accepted by Analysis and Math Physics journal, https://arxiv.org/abs/2402.11096
(292) Energy bounds for weighted spherical codes and designs via linear programming, (with Sergiy Borodachov, Peter Boyvalenkov, Peter Dragnev, Douglas Hardin, Maya Stoyanova) arXiv:2403.07457
(291) Universal minima of discrete potentials for sharp spherical codes, (with P. Boyvalenkov, P. Dragnev, D.P. Hardin and M. Stoyanova), submitted,
https://arxiv.org/pdf/2211.00092.pdf
(290) On Polarization of Spherical Codes and Designs (with P. Boyvalenkov, P. Dragnev, D.P. Hardin and M. Stoyanova), submitted
(288) Point source equilibrium problems with connections to weighted quadrature domains, (with P. Dragnev and A. Legg), Indag. Math. accepted.
(287) Threshold Condensation to Singular Support for a Riesz Equilibrium Problem (with Djalil Chafaï and Robert S. Womersley), Anal.Math.Phys. 13, 19 (2023). https://doi.org/10.1007/s13324-023-00779-w
(286) On the solution of a Riesz equilibrium problem and integral
identities for special functions (with Djalil Chafaï and Robert S. Womersley),
J. Math. Anal. and App., Volume 515, Issue 1, 1 November 2022, 126367
(285) Asymptotics of k-nearest neighbor Riesz energies (with D.P. Hardin and O.Vlasiuk) submitted
(284) Riesz Energy Problems with External Fields and Related Theory (with P. Dragnev, R. Orive and F. Wielonsky), Constr. Approx. to appear,
(283) Universal Bounds for Size and Energy of Codes of Given Minimum and Maximum Distances, (with P. Boyvalenkov, P. Dragnev, D.P. Hardin and M. Stoyanova), IEEE Trans. Inform Theory, accepted.
(282) Dynamics of particles on a curve with pairwise hyper-singular repulsion (with D. Hardin, R. Shu, E. Tadmor), Discrete Contin. Dyn. Syst., 41 (2021), no. 12, 5509-5536.
(281) Upper bounds for energies of spherical codes of given cardinality and separation,(with P. Boyvalenkov, P. Dragnev, D.P. Hardin and M. Stoyanova) Designs, Codes and Cryptography, vol. 88, 2020, 1811-1826.
(280) On the search for tight frames of low coherence, (with X. Chen and D. Hardin),
(279) On two problems concerning universal bounds for codes, (with P. Boyvalenkov, P. Dragnev, D.P. Hardin and M. Stoyanova) Proc. XVI International Symposium “Problems of Redundancy in Information and Control Systems”, 2019, 58-63.
(278) Linear programming bounds for energy and cardinality of codes of given min and max distances,(with P. Boyvalenkov, P. Dragnev, D.P. Hardin and M. Stoyanova) Proc. IEEE International Symposium on Information Theory, Paris, July 2019, 1747-1751 (https://ieeexplore.ieee.org/document/8849388)
(277) Bounds for spherical codes: the Levenshtein framework lifted (with P. Boyvalenkov, P. Dragnev, D.P. Hardin and M. Stoyanova), Math. Comp. to appear.
(276) Unconstrained Polarization (Chebyshev) Problems: Basic Properties and Riesz Kernel Asymptotics (with D. Hardin, and M. Petrache) Potential Analysis, 2020
https://doi.org/10.1007/s11118-020-09875-z.
Corrigendum
(273) Energy Bounds for Codes in Polynomial Metric Spaces (with P. Boyvalenkov, P. Dragnev, D.P. Hardin and M. Stoyanova), Analysis and Math Physics, 9(2), 781-808, 2019.
(272) Asymptotic Linear Programming Lower Bounds for the Energy of Minimizing Riesz and Gauss Configurations (with D.P. Hardin and T.J. Michaels), Mathematika, 65, 2019, no. 1, 157-180
(271) On spherical codes with inner products in a prescribed interval (with P. Boyvalenkov, P. Dragnev, D. Hardin, and M. Stoyanova), Des. Codes Cryptogr. 87 (2-3), 299–315, 2019. https://doi.org/10.1007/s10623-018-0524-z. [PDF]
(268) Local properties of Riesz minimal energy configurations and equilibrium measures (with D. Hardin, A. Reznikov and A. Volberg), International Math Research Notices IMRN 2019(16), 5066–5086 (2019) [PDF]
(267) Logarithmic and Riesz equilibrium for multiple sources on the sphere-the exceptional case (with J. Brauchart, P. Dragnev, and R. Womersley), In: Contemporary Computational Mathematics – a celebration of the 80th birthday of Ian Sloan (J. Dick, F. Y. Kuo, H. Wozniakowski, eds.),
Springer Nature, 179-204 (2018)
[PDF]
(266) Large deviation principles for hypersingular Riesz gases (with D.P. Hardin, T. Leblé, and S. Serfaty), Constr. Approx., 48(1), 2018, 61–100. [PDF]
(265) Covering and separation of Chebyshev points for non-integrable Riesz potentials
(with A. Reznikov and A. Volberg), J. Complexity, 46 (2018), 19-44 [PDF]
(264) A Minimum Principle for Potentials with Application to Chebyshev Constants (with A. Reznikov), Potential Analysis, 47 (2017), no. 2, 235–244 [PDF]
(262) A Comparison of Popular Point Configurations on S^2 (with D. Hardin and T. Michaels), Dolomites Research Notes on Approximation, vol.9, 2016, 16-49.
[PDF]
(261) Optimal discrete measures for Riesz potentials, (with Sergiy V Borodachov, Douglas P. Hardin, Alexander Reznikov) Trans. Amer. Math. Soc., 370(10), 2018, 6973-6993. [PDF]
(260) Generating Point Configurations via Hypersingular Riesz Energy with an External Field (with D. Hardin and O. Vlasiuk) SIAM J. Math. Analysis, 49 (2017), no. 1, 646–673. [PDF]
(259) Random Point Sets on the Sphere-Hole Radii, Covering, and Separation (with J. Brauchart, A. Reznikov, I. Sloan, Y.G. Wang and R. Womersley) Experimental Math, 27 (2018), no. 1, 62-81. [PDF]
(258) Universal Upper and Lower Bounds on Energy of Spherical Designs (with P.G. Boyvalenkov, P. Dragnev, D. Hardin, and M. Stoyanova, Dolomites Research Notes on Approximation, vol. 8, 2015, 51-65. [PDF]
(257) Energy Bounds for Codes and Designs in Hamming Spaces (with P.G. Boyvalenkov, P. Dragnev, D. Hardin, and M. Stoyanova) Designs, Codes and Cryptography, Des. Codes Cryptogr. 82 (2017), no. 1-2, 411–433. 94B65 . [PDF]
(256) Next Order Energy Asymptotics for Riesz Potentials on Flat Tori”
(with D. Hardin, E. Saff, B. Simanek and Y. Su) Int. Math. Res. Not. IMRN 2017, no. 12, 3529–3556.[PDF]
(255) Minimum Riesz Energy Problems for a Condenser with “Touching Plates” (with P. Dragnev, B.Fuglede, D. Hardin, and N. Zorii), Potential Analysis (to appear) [PDF]
(254) The Covering Radius of Randomly Distributed Points on a Manifold (with A. Reznikov), Int. Math. Res. Not. IMRN 2016, no. 19, 6065–6094. [PDF]
(253) Universal Lower Bounds for Potential Energy of Spherical Codes (with P. Boyvalenkov, P. Dragnev, D. Hardin, and M. Stoyanova), Constr. Approx. 44 (2016), no. 3, 385–415. [PDF]
(252) Covering of Spheres by Spherical Caps and Worst-Case Error for Equal
Weight Cubature in Sobolev Spaces (with J. S. Brauchart, J. Dick, I. H. Sloan, YG. Wang and R. S. Womersley), J. Math. Anal. Appl. 431 (2015), no. 2, 782–811. [PDF]
(249) Periodic Discrete Energy for Long-Range Potentials (with D. Hardin and B. Simanek), J. Math Physics, 55, 123509 (2014) [PDF]
(248) An Electrostatics Problem on the Sphere Arising from a Nearby Point Charge (with J. Brauchart and P. Dragnev), In: Constructive Theory of Functions (ed. K. Ivanov, G. Nikolov, R. Uluchev), Sozopol 2013, pp. 11-55, Drinov Academic Publishing House, Sofia, (2014) [PDF]
(247) Riesz External Field Problems on the Hypersphere and Optimal Point Separation (with J. Brauchart and P. Dragnev), Potential Analysis, vol. 41 (2014), 647–678.
[PDF]
(246) Inverse Bernstein Inequalities and Min-Max-Min Problems on the Unit Circle (with T. Erdelyi and D. Hardin), Mathematika, vol. 61 (2015), no. 3, 581–590. [PDF]
(245) Low Complexity Methods for Discretizing Manifolds via Riesz Energy Minimization (with S. Borodachov and D. Hardin), Found. Comput. Math. 14 (2014), no. 6, 1173–1208.[PDF]
(244) Reverse Triangle Inequalities for Riesz Potentials and Connections with Polarization (with I. Pritsker and W. Wise), J. Math. Anal. Appl. 410 (2014), no. 2, 868–881.[PDF]
(242) Mesh Ratios for Best-Packing and Limits of Minimal Energy Configurations (with A. Bondarenko and D. Hardin), Acta Math. Hungar. 142 (2014), no. 1, 118–131. [PDF]
(240) QMC Designs: Optimal Order Quasi Monte Carlo Integration Schemes on the Sphere (with J.S. Brauchart, I.H. Sloan, and R.S. Womersley), Math. Comp. 83 (2014), no. 290, 2821–2851. Math. Comp. 83 (2014), no. 290, 2821–2851.[PDF]
(239) Polarization Optimality of Equally Spaced Points on the Circle for Discrete Potentials (with D. Hardin and A. Kendall), Discrete Comput. Geom. 50 (2013), no. 1, 236–243. [PDF]
(238) Riesz polarization in higher dimensions (with T. Erdelyi), J. Approx. Theory, vol. 171 (2013), 128-147. [PDF]
(235) The Next-Order Term for Minimal Riesz and Logarithmic Energy Asymptotics on the Sphere (with J.S. Brauchart and D.P. Hardin), Contemp. Math., Vol. 578 (2012), 31-61. [PDF]
(233) Quasi-uniformity of Minimal Weighted Energy Points (with D. Hardin and T. Whitehouse), Journal of Complexity. Vol. 28, Issue 2, (2012), 177-191. [PDF]
(232) A Fascinating Polynomial Sequence Arising From An Electrostatics Problem on the Sphere (with J.S. Brauchart, P.D. Dragnev, and C.E. Van de Woestijne), Acta Mathematica Hungarica: Volume 137, Issue 1 (2012), Page 10-26. [PDF]
(229) Minimal N-Point Diameters and f-Best-Packing Constants in R^d (with A.V. Bondarenko and D.P. Hardin), Proceedings American Mathematics Society. vol. 142, Issue 3 (2014), 981-988.[PDF]
(228) Discrete Energy Asymptotics on a Riemannian Circle (with J.S. Brauchart and D.P. Hardin), Uniform Distribution Theory, vol. 7, no. 2, (2012), 77-108. [PDF]
(226) Riesz Extremal Measures on the Sphere for Axis-Supported External Fields (with J.S. Brauchart and P.D. Dragnev), J. Math. Anal. Appl., 356 (2009), 769-792. [PDF]
(225) Asymptotics of Greedy Energy Points (with Abey Lopez), Math. Comp. vol. 79 (2010), 2287-2316. [PDF]
(223) The Riesz Energy of the N-th Roots of Unity: An Asymptotic Expansion for Large N (with J.S. Brauchart and D.P. Hardin), Bull. London Math. Soc., 41 (2009), 621-633. [PDF]
(221) Riesz Energy and Sets of Revolution in R^3 (with Johann S. Brauchart and Douglas P. Hardin), In Functional Analysis and Complex Analysis, 47-57, Contemp. Math., 481, Amer. Math. Soc., Providence, RI, 2009.[PDF]
(217) Asymptotics of Weighted Best-Packing on Rectifiable Sets (with S. V. Borodachov and D. P. Hardin), (Russian) Mat.Sb. 199 (2008), no. 11, 3-20; translation in Sb. Math. 199 (2008), no. 11-12, 1579-1595. [PDF]
(216) The Support of the Limit Distribution of Optimal Riesz Energy Points on Sets of Revolution in R3 (with J. Brauchart and D. Hardin), J. Math. Phys, 48 (2007), no. 12, 122901, 24 pp. [PDF]
(215) Menke Points on the Real Line and Their Connection to Classical Orthogonal Polynomials (with P. Mathur and J.S. Brauchart), J. Comput. Appl. Math., 233 (2010), 1416-1431. [PDF]
(212) Asymptotics of Best-Packing on Rectifiable Sets (with S.V. Borodachov and D.P. Hardin), Proc. Amer. Math. Soc., Vol. 135 (2007), pp. 2369-2380. [PDF]
(211) Riesz Spherical Potentials with External Fields and Minimal Energy Points Separation (with P. Dragnev), Potential Anal., Vol. 26, No. 2 (2007), pp. 139-162. [PDF]
(210) The Support of the Logarithmic Equilibrium Measure on Sets of Revolution in R3 (with D. Hardin and H. Stahl), J. Math. Phys., Vol. 48, No. 2 (2007), 122901, 14 pp. [PDF]
(208) Asymptotics for Discrete Weighted Minimal Riesz Energy Problems on Rectifiable Sets (with S.V. Borodachov and D.P. Hardin), Trans. Amer. Math. Soc., Vol. 360 (2008), pp. 1559-1580. [PDF]
(205) On Separation of Minimal Riesz Energy Points on Spheres in Euclidean Spaces (with A. B. J. Kuijlaars and X. Sun), Journal Comp. & Applied Math., Vol 199, No. 1 (2007), pp. 172-180. [PDF]
(201) Discretizing Manifolds via Minimum Energy Points
(with Doug Hardin), Notices of the American Mathematical Society, Vol. 51, No. 10 (2004), pp. 1186-1194. [PDF]
(199) Minimal Riesz Energy Point Configurations for Rectifiable d-Dimensional Manifolds
(with Doug Hardin), Advances in Mathematics, Vol. 193, No. 1 (2005), pp. 174-204. [PDF]
(196) Asymptotics for Minimal Discrete Riesz Energy on Curves in Rd
(with A. Martínez-Finkelshtein, V. Maymeskul, and E.A. Rakhmanov), Canadian Journal of Mathematics, Vol. 56 (2004), pp. 529-552. [PDF]
(192) Note on d-extremal configurations for the Sphere in R(d+1)
(with M. Goetz), Recent progress in multivariate approximation, Internat. Ser. Numer. Math., Birkhauser, Basel, Vol. 137 (2001), pp. 159-162. [PDF]
(161) Distributing Many Points on a Sphere
(with A.B.J. Kuijlaars), The Mathematical Intelligencer, Vol. 19, No. 1 (1997), pp. 5-11. [PDF][/p>
(159) Asymptotics for Minimal Discrete Energy on the Sphere
(with A.B.J. Kuijlaars), Transactions of the American Mathematical Society, Vol. 350, No. 2 (1998), pp. 523-538. [PDF]
(156) Electrons on the Sphere
(with E.A. Rakhmanov and Y.M. Zhou), Computational Methods and Function Theory, (R. M. Ali, S. Ruscheweyh, and E. B. Saff, eds.), World Scientific, (1995), pp. 293-309. [PDF]
(155) Minimal Discrete Energy on the Sphere
(with E.A. Rakhmanov and Y.M. Zhou), Mathematical Research Letters, Vol. 1 (1994), pp. 647-662. [PDF]
Spiral Points on the Sphere
The spiral point algorithm developed by Rahkmanov, Saff, and Zhou has been improved by Knud Thomsen as follows:
Initialize:
p = 1/2
a = 1 – 2*p/(n-3)
b = p*(n+1)/(n-3)
r(1) = 0
theta(1) = pi
phi(1)) = 0
Then for k stepping by 1 from 2 to n-1:
k’ = a*k + b
h(k) = -1 + 2*(k’-1)/(n-1)
r(k) = sqrt(1-h(k)^2)
theta(k) = arccos(h(k))
phi(k) = [phi(k-1) + 3.6/sqrt(n)*2/(r(k-1)+r(k))] (mod 2*pi)
Finally:
theta(n) = 0
phi(n) = 0
See
http://groups.google.com/group/sci.math/browse_thread/thread/983105fb1ced42c/e803d9e3e9ba3d23#e803d9e3e9ba3d23
Code for Equal-Area Points on Sphere
EQ Sphere Partititions and Recursive Zonal Equal Area (EQ) Sphere Partitioning Toolbox: http://eqsp.sourceforge.net
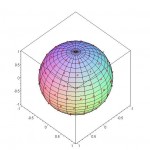
100 Equal – Area Points on a Sphere
Full Size: [JPG]
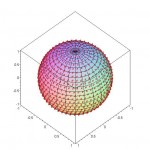
1000 Equal – Area Points on a Sphere
Full Size: [JPG]
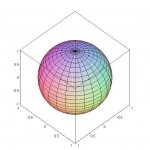
10000 Equal – Area Points on a Sphere
Full Size: [JPG]
Poppy-Seed Bagel Theorem
Wikipedia
Science & Vie Profile
Science & Vie, July 2005.
Poppy Seed Bagel Math
National Public Radio, Weekend Edition, December 11, 2004.
The Poppy-Seed Bagel Theorem
Exploration, The Online Research Journal of Vanderbilt University, November 30, 2004.
Discretizing Manifolds via Minimum Energy Points
Notices of the American Mathematical Society, November, 2004.
Rob Womersley’s Visualization of Minimum Energy Points on the Torus

©2024 Vanderbilt University ·
Site Development: University Web Communications