Challenge Name
Once upon a time, there was an intra-axonal signal untouched by the noise…
Purpose and relevance of the challenge
The aim of this challenge is to retrieve as much microstructural information in white matter (WM) as possible using diffusion MRI (dMRI) signal in the q–t space. The synthetic dMRI signal based on Monte Carlo simulations of diffusion within realistic axonal shapes will be provided to participants. The intra-axonal space has been segmented from a sequential-slice electron microscopy dataset of the mouse brain corpus callosum [1]. To keep things simple in this complex world, extra-axonal signal is ignored; the noise is largely reduced by including as many random walkers as possible (tens of million) in simulations; and the dMRI sequence is an ideal narrow-pulse monopolar PGSE, ![]() , simulated for a wide range of diffusion times t and diffusion wave vectors q in 3 dimensions.
, simulated for a wide range of diffusion times t and diffusion wave vectors q in 3 dimensions.
Challenge Tasks:
- Estimate the fiber orientation dispersion in terms of its spherical harmonics (SH) coefficients
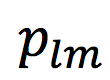 up to
up to 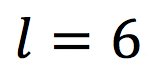 . Note that the ground truth of axonal orientation distribution function (ODF) will be different from that in [1], as we will re-arrange a subset of the segmented axons in space.
. Note that the ground truth of axonal orientation distribution function (ODF) will be different from that in [1], as we will re-arrange a subset of the segmented axons in space.
- Estimate as many moments of axonal diameter distribution as possible; reconstruct axonal diameter distribution based on dMRI signal. Note that the axonal diameter varies along each individual axon, and different axons in a set have different shapes [1]. For the purpose of this challenge, the ground truth of the diameter distribution will be constructed by pooling the histograms of diameters determined from multiple cross-sections of each axon. The effective diameter in each cross-section will be defined as the equivalent circle diameter
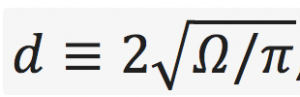 , where
, where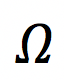 is the cross-sectional area; cross-sections are taken normal to the local axonal direction. It is up to the participants to understand which “parts” of the provided dMRI propagator are responsible for which moment of the distribution.
is the cross-sectional area; cross-sections are taken normal to the local axonal direction. It is up to the participants to understand which “parts” of the provided dMRI propagator are responsible for which moment of the distribution.
Datasets
The dataset of this challenge consist of a simulated dMRI signal in the realistic intra-axonal space. The cell membrane of axons is assumed impermeable, with no surface relaxation in simulations. Three datasets of different fiber orientation dispersion will be provided. For each dataset, 100 segmented axons will be selected to simulate signals of monopolar PGSE for 10 b-values (60 gradient directions for each shell) and 1000 diffusion times in a wide range.
The segmentation pipeline and the principles of Monte Carlo simulations for microstructural imaging are described in [1] and [2].
Link to Data : See Registration and Data Access page
Participation (Data given to participants)
The task of this challenge is (1) to estimate the fiber orientation dispersion and (2) to estimate different moments of the axonal diameter distribution. The two datasets with different tissue parameters will be saved in text files, and a MATLAB code will be provided for the data visualization. Signals of monopolar PGSE in multiple b-values and diffusion times will be simulated with minimal noise.
Submission
Participants need to submit the following tissue parameters for each dataset: rotational invariants ![]() of SH coefficients up to
of SH coefficients up to ![]() (Ref [3] and below for the definition), and the first few moments of axonal diameter
(Ref [3] and below for the definition), and the first few moments of axonal diameter ![]() (µm), e.g.,
(µm), e.g., ![]() ,
, ![]() , and so on.
, and so on.
The moments of the inner diameter is calculated based on the equivalent
circle diameter of the segmented realistic intra-axonal space in the mouse
brain genu of corpus callosum [1].
The rotational invariant of the fiber orientation dispersion is calculated
based on the definition in Eq. (4) and Eq. (5) of [3].
Thus the diameter moments will be estimated and the rotational invariants are to be estimated (submitted separately). Each submission should contain:
For diameter moment estimation:
1. submission.txt: 3×3 matrix saving the moments of the inner diameter
(<d>, <d^2>, and <d^4> for each column) for the three voxels (each row).
2. info.txt (team and submission information)
For rotational invariant estimation:
1. submission.txt: 3×3 matrix saving the rotational invariants of the fiber orientation dispersion (p2, p4, and p6 for each column) for the three voxels (each row).
2. info.txt (team and submission information)
Evaluation
The ground truth values will be calculated based on the realistic microstructure of selected axons, analyzed as in [1]. Particularly, for the part 1 (ODF), we will compare the rotational invariants ![]() for each
for each ![]() [3]:
[3]:
![]()
where ![]() ,and
,and ![]() . For the ODF normalization,
. For the ODF normalization, ![]() under this definition. For the part 2 (axon size), we will compare the moments of axonal diameter (µm), such as
under this definition. For the part 2 (axon size), we will compare the moments of axonal diameter (µm), such as ![]() ,
, ![]() , and so on. The realistic axonal shape and the analysis tool will be open source. We will rank the submission according to the accuracy.
, and so on. The realistic axonal shape and the analysis tool will be open source. We will rank the submission according to the accuracy.
References
- Hong-Hsi Lee, Katarina Yaros, Jelle Veraart, Jasmine L. Pathan, Feng-Xia Liang, Sungheon G. Kim, Dmitry S. Novikov, and Els Fieremans. Along-axon diameter variation and axonal orientation dispersion revealed with 3D electron microscopy: implications for quantifying brain white matter microstructure with histology and diffusion MRI. Brain Structure and Function (2019). doi.org/10.1007/s00429-019-01844-6
- Els Fieremans, Hong-His Lee. Physical and numerical phantoms for the validation of brain microstructural MRI: A cookbook. NeuroImage (2018). doi.org/10.1016/j.neuroimage.2018.06.046
- Dmitry S. Novikov, Jelle Veraart, Ileana O. Jelescu, Els Fieremans. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. NeuroImage (2018). doi.org/10.1016/j.neuroimage.2018.03.006
How to get the data
Please see “Registration and Data Access” Page.
Sub-challenge Chairs
Hong-Hsi Lee <New York University>
Dmitry S Novikov <New York University>
Els Fieremans <New York University>
