A numerical formulation aimed at modeling the nonlinear response of elastic materials using large deformation continuum mechanics in three dimensions is developed. This finite element formulation is based on the Eulerian description of motion and the transport of the deformation gradient. When modeling a nearly incompressible solid, the transport of the deformation gradient is decomposed into its isochoric part and the Jacobian determinant as independent fields. A homogeneous isotropic hyperelastic solid is assumed and B-splines-based finite elements are used for the spatial discretization. A variational multiscale residual-based approach is employed to stabilize the transport equations. The performance of the scheme is explored for both compressible and nearly incompressible applications. The numerical results are in good agreement with theory illustrating the viability of the computational scheme.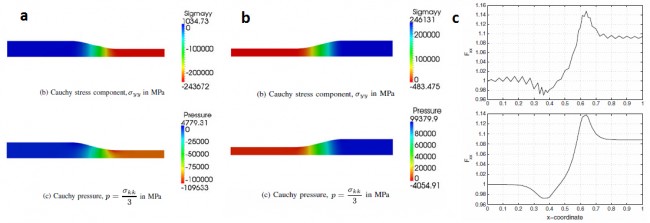Simulated cold rolling and cold expansion of steel ingots. Figures a and b show the variation of Cauchy stress in the ingots. Figure c shows the results without (bottom) and with (top) variational multiscale stabilization of the governing equations. The stabilization introduced is able to remove completely the spurious oscillations and thus gives an accurate estimate of the stresses and pressure in the material.