A discrete damage zone model aimed at simulating fracture initiation and propagation within the framework of the finite element method is proposed. The approach is related to the discrete cohesive zone models where cohesive laws (also known as traction-separation laws) are introduced through a set of nonlinear springs attached to the finite element nodes where fracture is assumed to occur. In the proposed approach, rather than employing specific cohesive laws at the element edges, we employ damage laws to prescribe both interface spring softening and bulk material stiffness degradation to study crack propagation. For a homogeneous isotropic material the same damage law is assumed to hold in both the continuum and the interface elements. Accordingly, three scalar damage variables are introduced, one to model the damage of the continuum and the other two to model the degradation of the discrete spring elements. The parameters of the assumed damage law are calculated from the principles of linear elastic fracture mechanics. The proposed discrete damage zone model (DDZM) is implemented in Abaqus via the user defined element (UEL) subroutine. Numerical results for single-mode and mixed-mode delamination are presented. The results are in good agreement with those obtained from the virtual crack closure technique (VCCT) and available analytical solutions, thus, illustrating the validity of this approach. Finally, the suitability of the method for studying fracture in fiber-matrix composites involving fiber debonding and matrix cracking is illustrated.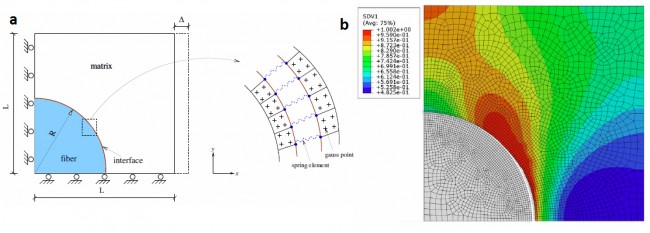Fracture in fiber-matrix composites involving fiber debonding as well as matrix cracking. Figure a shows the geometry and dimensions of the square unit cell and the zoom of the discrete elements near fiber-matrix interface. Figure b shows the numerical result wherein the ultimate failure of the unit cell occurs through a combination of breaking of spring elements and continuum damage in finite elements.