Biofilm growth in fluid media

A continuum model for the biofilm growth in a generalized non-dimensional form is developed, based on the 1D kinetic model proposed by (Chopp et al. 2002). The model considers fluid flow around the biofilm surface, the advection–diffusion and reaction of substrate, variable biomass, volume fraction and erosion due to the interfacial shear stress at the biofilm–fluid interface. A combined extended finite element and level set method is used to simulate biofilm growth. The model gives quantitative results for the given kinetic model and is useful for understanding the biofilm growth behavior and biofilm architecture. This work illustrates that detachment criteria which are based on the shape of the biofilm structure only (i.e. based on biofilm height) that do not take local flow effects into account are not appropriate. The model suggests that erosion loss at the biofilm-fluid interface is more significant than detachment events involving the tearing of the entire biofilm near the substratum.

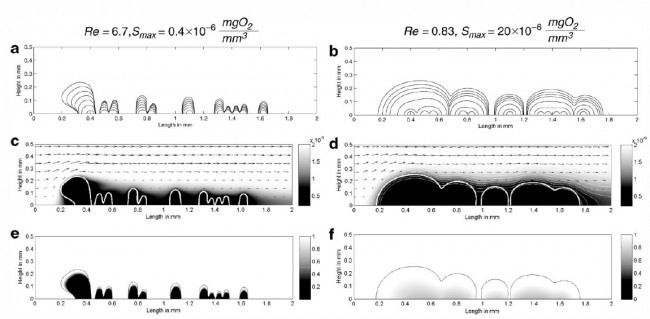
Simulated biofilm growth. a: Biofilm interface at t = 0, 20, 40, 60, 80, 100, 120 days. b: Biofilm interface at t = 0, 1.0, 2.0, 3.0, 3.5, 4.0, 4.5 days. c: Fluid flow velocity field and substrate concentration in the flow cell at t = 120 days. d: Fluid flow velocity field and substrate concentration in the flow cell at t = 4.5 days. e: Biomass fraction at t = 120 days. f: Biomass fraction at t = 4.5 days.

Microstructure evolution in elastic media

A sharp-interface numerical formulation using an Eulerian description aimed at modeling diffusional evolution of precipitates produced by phase transformations in elastic media is developed. The extended finite element method (XFEM) is used to solve the field equations and the level set method is used to evolve the precipitate–matrix interface. This new formulation is capable of handling microstructures with arbitrarily shaped particles and capturing their topological transitions without needing the mesh to conform with the precipitate–matrix interface. The XFEM makes it possible to model the precipitate and the matrix to be both elastically anisotropic and inhomogeneous with ease. The interface evolution velocity is evaluated using a domain integral scheme that is consistent with the sharp interface. Numerical examples modeling two distinct phases of particle evolution, growth (dendritic evolution) and equilibration (Ostwald ripening) are presented. To overcome the issue of grid anisotropy in growth simulations, a random grid rotation scheme is implemented in conjunction with a bicubic spline interpolation scheme. Growing shapes are dendritic while equilibrium shapes are squarish and in this respect our simulation results are in agreement with those presented in the literature

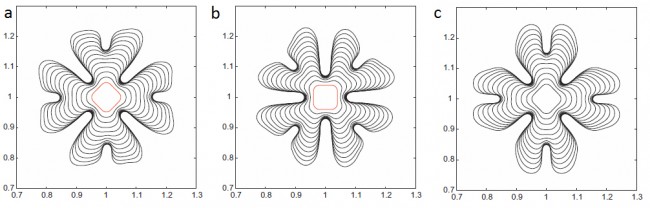
Simulated precipitate growth. The model considers purely dilatational misfit strain and isotropic surface energy for the precipitates. Initial particle size is 0.04 m. The first two results in figures a and b obtained using a random grid rotation scheme are in good agreement with each other. The third result in figure c is obtained without using grid rotation. It is clear that grid anisotropy alters the shape of the precitipate and the grid rotation scheme successfully ameliorates the results.

Finite strain hyperelasticity

A numerical formulation aimed at modeling the nonlinear response of elastic materials using large deformation continuum mechanics in three dimensions is developed. This finite element formulation is based on the Eulerian description of motion and the transport of the deformation gradient. When modeling a nearly incompressible solid, the transport of the deformation gradient is decomposed into its isochoric part and the Jacobian determinant as independent fields. A homogeneous isotropic hyperelastic solid is assumed and B-splines-based finite elements are used for the spatial discretization. A variational multiscale residual-based approach is employed to stabilize the transport equations. The performance of the scheme is explored for both compressible and nearly incompressible applications. The numerical results are in good agreement with theory illustrating the viability of the computational scheme.

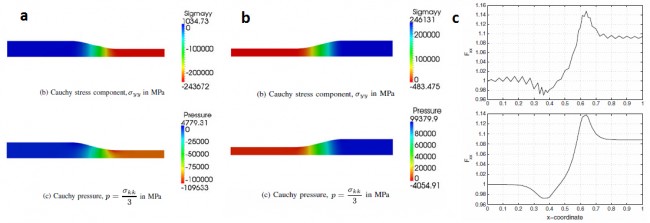
Simulated cold rolling and cold expansion of steel ingots. Figures a and b show the variation of Cauchy stress in the ingots. Figure c shows the results without (bottom) and with (top) variational multiscale stabilization of the governing equations. The stabilization introduced is able to remove completely the spurious oscillations and thus gives an accurate estimate of the stresses and pressure in the material.

Tertiary creep damage model for polycrystalline ice

A continuum damage model for the temperature dependent creep response of polycrystalline ice under a multiaxial state of stress, suited for ice in polar regions, is developed. The proposed model is based on a thermo-viscoelastic constitutive law for ice creep and a local orthotropic damage accumulation law for tension, compression and shear loadings. Orthotropic damage is represented by a symmetric second-order damage tensor and its effect on creep is incorporated through the effective stress concept. The unknown model parameters are first calibrated using published experimental data from constant uniaxial stress tests under pure compressive and pure tensile loadings; and then, predictions are made for constant strain rate and multiaxial loadings. The predicted results are in good agreement with both experimental and numerical results in the literature illustrating the viability of the proposed model. The model captures the temperature dependence of material strength and asymmetric mechanical behavior under tension and compression. The model is mainly intended for studying the failure mechanisms of polar ice at low deformation rates with depth varying temperature profiles.

Model fit to experimental data and parameter calibration. Figures a and b show the asymmetric behavior of ice under pure compressive and tensile loadings. Figure c shows the temperature dependence of material behavior of ice.

Mixed mode fracture in composites

A discrete damage zone model aimed at simulating fracture initiation and propagation within the framework of the finite element method is proposed. The approach is related to the discrete cohesive zone models where cohesive laws (also known as traction-separation laws) are introduced through a set of nonlinear springs attached to the finite element nodes where fracture is assumed to occur. In the proposed approach, rather than employing specific cohesive laws at the element edges, we employ damage laws to prescribe both interface spring softening and bulk material stiffness degradation to study crack propagation. For a homogeneous isotropic material the same damage law is assumed to hold in both the continuum and the interface elements. Accordingly, three scalar damage variables are introduced, one to model the damage of the continuum and the other two to model the degradation of the discrete spring elements. The parameters of the assumed damage law are calculated from the principles of linear elastic fracture mechanics. The proposed discrete damage zone model (DDZM) is implemented in Abaqus via the user defined element (UEL) subroutine. Numerical results for single-mode and mixed-mode delamination are presented. The results are in good agreement with those obtained from the virtual crack closure technique (VCCT) and available analytical solutions, thus, illustrating the validity of this approach. Finally, the suitability of the method for studying fracture in fiber-matrix composites involving fiber debonding and matrix cracking is illustrated.

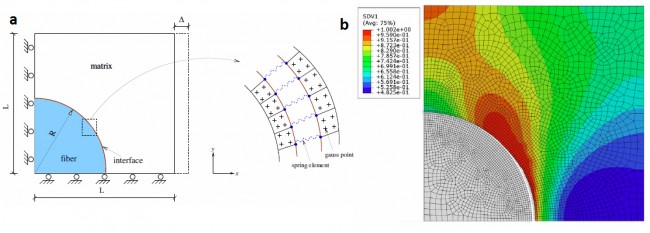
Fracture in fiber-matrix composites involving fiber debonding as well as matrix cracking. Figure a shows the geometry and dimensions of the square unit cell and the zoom of the discrete elements near fiber-matrix interface. Figure b shows the numerical result wherein the ultimate failure of the unit cell occurs through a combination of breaking of spring elements and continuum damage in finite elements.