A sharp-interface numerical formulation using an Eulerian description aimed at modeling diffusional evolution of precipitates produced by phase transformations in elastic media is developed. The extended finite element method (XFEM) is used to solve the field equations and the level set method is used to evolve the precipitate–matrix interface. This new formulation is capable of handling microstructures with arbitrarily shaped particles and capturing their topological transitions without needing the mesh to conform with the precipitate–matrix interface. The XFEM makes it possible to model the precipitate and the matrix to be both elastically anisotropic and inhomogeneous with ease. The interface evolution velocity is evaluated using a domain integral scheme that is consistent with the sharp interface. Numerical examples modeling two distinct phases of particle evolution, growth (dendritic evolution) and equilibration (Ostwald ripening) are presented. To overcome the issue of grid anisotropy in growth simulations, a random grid rotation scheme is implemented in conjunction with a bicubic spline interpolation scheme. Growing shapes are dendritic while equilibrium shapes are squarish and in this respect our simulation results are in agreement with those presented in the literature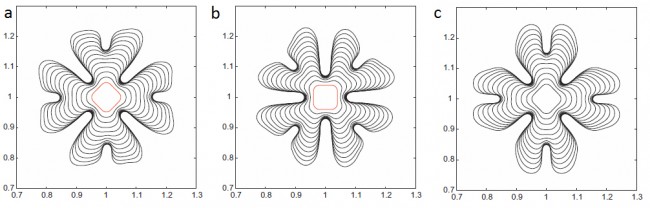Simulated precipitate growth. The model considers purely dilatational misfit strain and isotropic surface energy for the precipitates. Initial particle size is 0.04 m. The first two results in figures a and b obtained using a random grid rotation scheme are in good agreement with each other. The third result in figure c is obtained without using grid rotation. It is clear that grid anisotropy alters the shape of the precitipate and the grid rotation scheme successfully ameliorates the results.