Multiscale Modeling of Wave Propagation in Viscoelastic Phononic Crystals and Acoustic Metamaterials
Research Sponsor:
US National Science Foundation
Investigators:
Ruize Hu and Caglar Oskay
Motivation
-
Phononic crystals and acoustic metamaterials exhibit extraordinary capability in controlling
acoustic and elastic waves by manipulating band gaps that forbid waves to propagate within
targeted frequency ranges.
-
Modeling of transient wave propagation in these composites using direct numerical simulations is computationally prohibitive for structural design and analysis.
Objective
- Develop a multiscale computational framework for efficient modeling of transient wave propagation in periodic viscoelastic composites, capturing wave dispersion and bandgap phenomenon.
-
Investigate the effects of microstructural morphology, elastic and viscoelastic constituent material properties on the overall wave attenuation behavior.
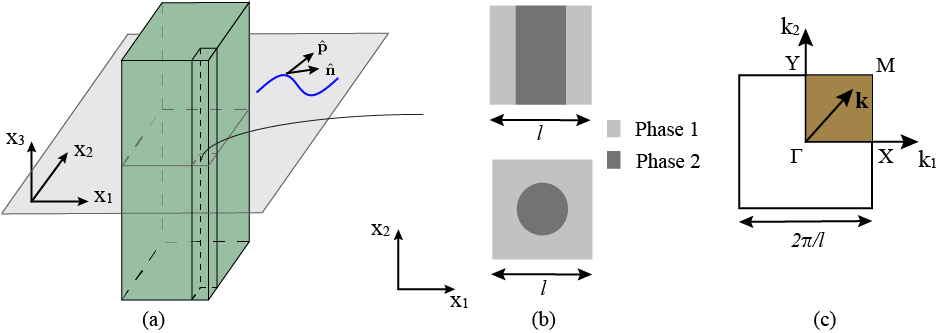
Spatial-temporal nonlocal homogenization model (STNHM)
High order asymptotic expansion
- Critical in extending the classical homogenization theory to short wavelength regime.
- Introduce spatial nonlocal terms in momentum balance equations at successive orders.
Construction of gradient-type nonlocal governing equation
- Derive temporal nonlocal terms in high symmetry directions of the first Brillouin zone.
- Nonlocal model parameters are uniquely determined by minimization of asymptotic residual.
Nonlocal effective medium model (NEM)
- Governing equation in the second order form with nonlocal features retained by the frequency-dependent nonlocal effective moduli tensor.
- Simulation of transient wave propagation without need of high order boundary conditions.
Dispersion relation
- Captures the acoustic branch, the stop band and the first optical branch in high symmetry directions.
- Evanescent wavenumber is predicted within the stop band.
Anti-plane shear wave
In-plane wave
Transient wave propagation
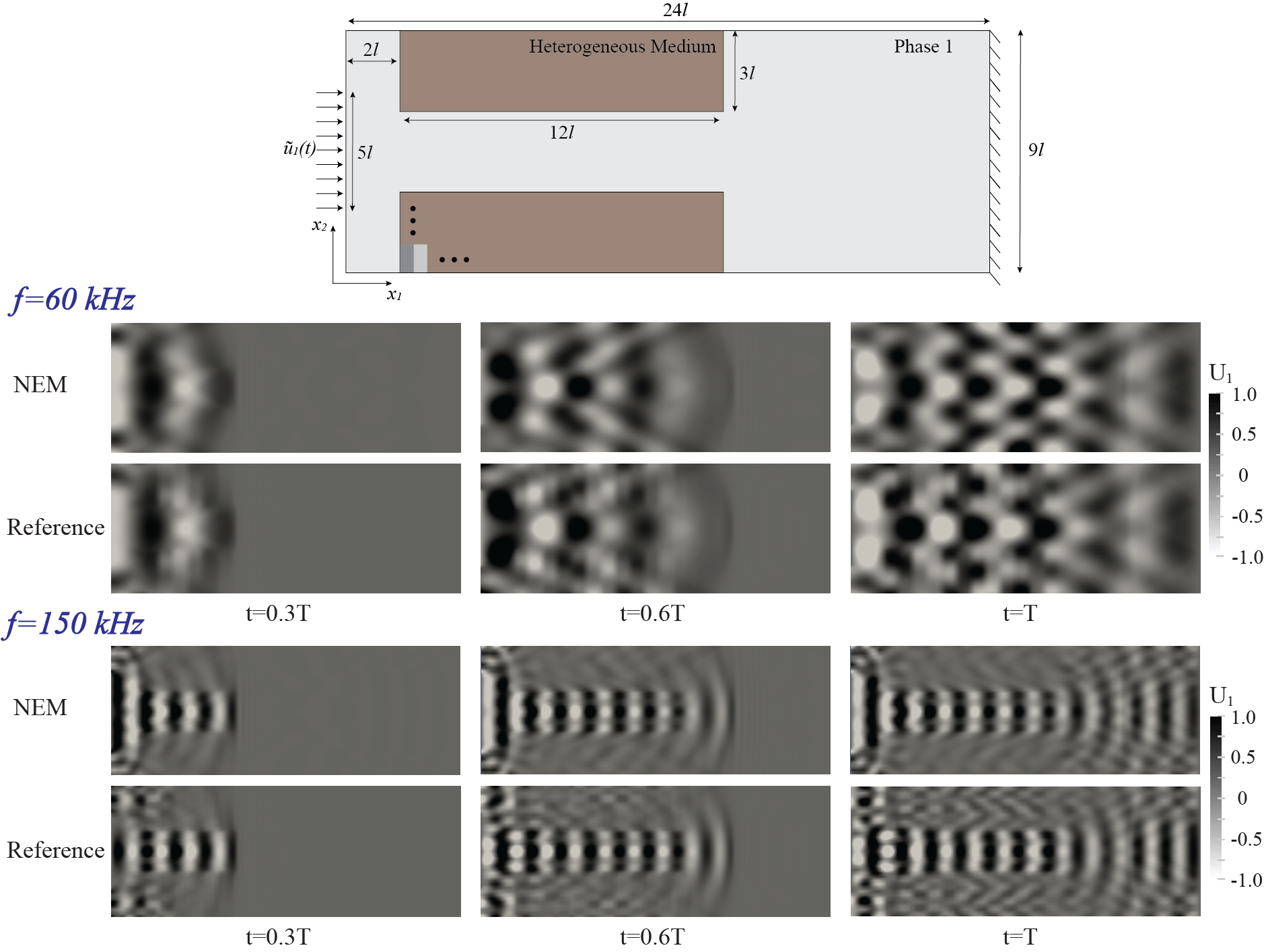
In-plane elastic waveguide modeling
- Wave dispersion occurs at relatively low frequency.
- Highly confined wave propagation when wave frequency is within the stop band.
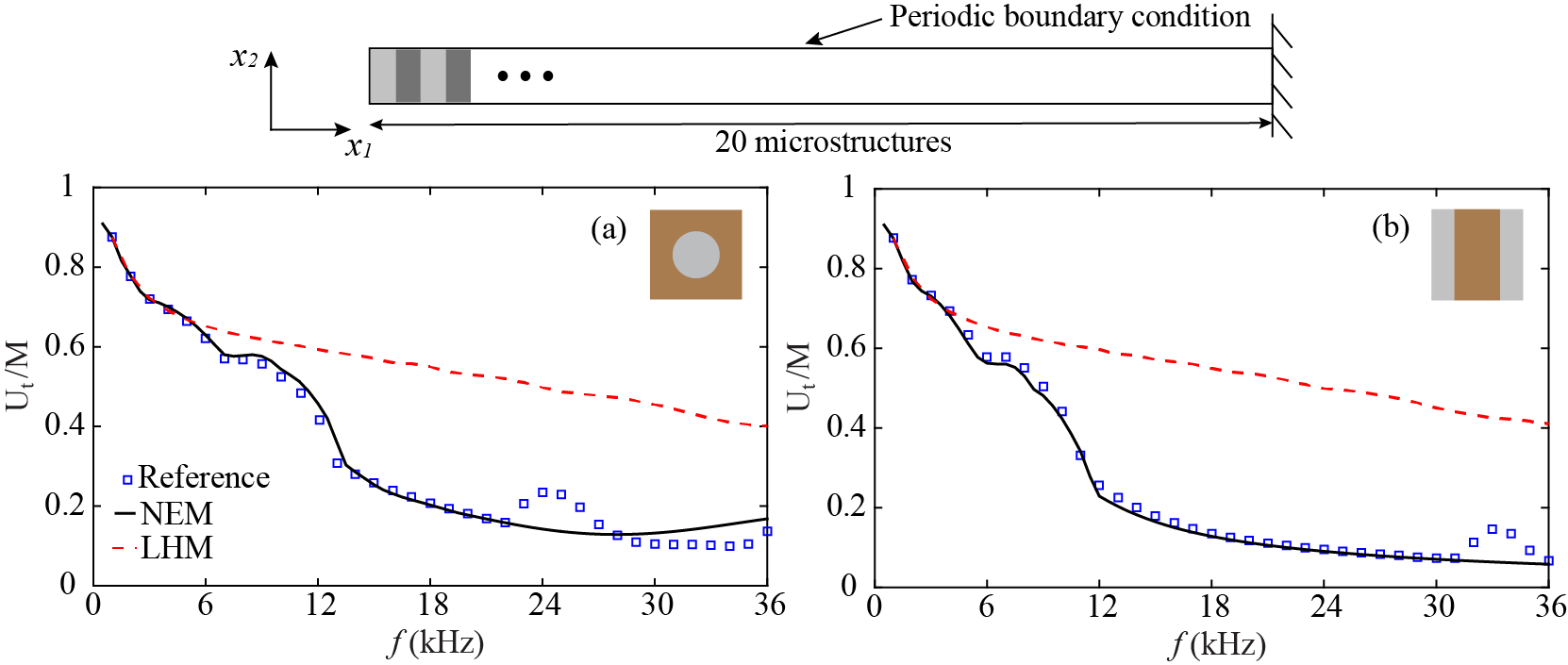
Anti-plane shear wave propagation in viscoelastic phononic crystal
- Nearly complete attenuation due to band gap formation and viscoelastic dissipation.
- Stronger attenuation compared to elastic phononic crystal.
- Compared to having viscoelastic dissipation only (LHM), band gap formation significantly improves wave attenuation.
- Layered microstructure has wider stop band and stronger wave attenuation within the stop band.