• modeling their inherent multiscale nature,
• capturing the complex interacting failure modes,
• extending models to rate-dependent loadings, and
• incorporating the high variability from manufacturing and the nature of the material in failure predictions.

Research Goal and Objectives

Goals:

• Gain a fundamental understanding of the sources of uncertainty in composite structures at all meaningful size scales.
• Gain a fundamental understanding of the mechanical phenomena at the micro- and macroscale which govern failure response for fiber reinforced polymer composites.
• Implement a failure prediction methodology which incorporates stochastic effects. beginning at the microscopic constituent scale and propagating up to the macroscopic structural scale.

Objectives – Mechanical modeling of composite structures:

• Implement a rate-dependent damage evolution law for modeling of constituent material response.
• Employ reduced order homogenization to efficiently capture the multiscale behavior of the composites.
• Utilize parallel computing structures to further speed up multiscale analyses.

Objectives – Uncertainty Quantification

• Calibrate constituent material parameters from experimental results from laminated composites using Bayesian methods.
• Make stochastic predictions of laminated composite failure from the calibrated constituent parameters.
• Characterize the length scale effects in the spatial variability of underlying material parameters.

Uncertainty in Composites

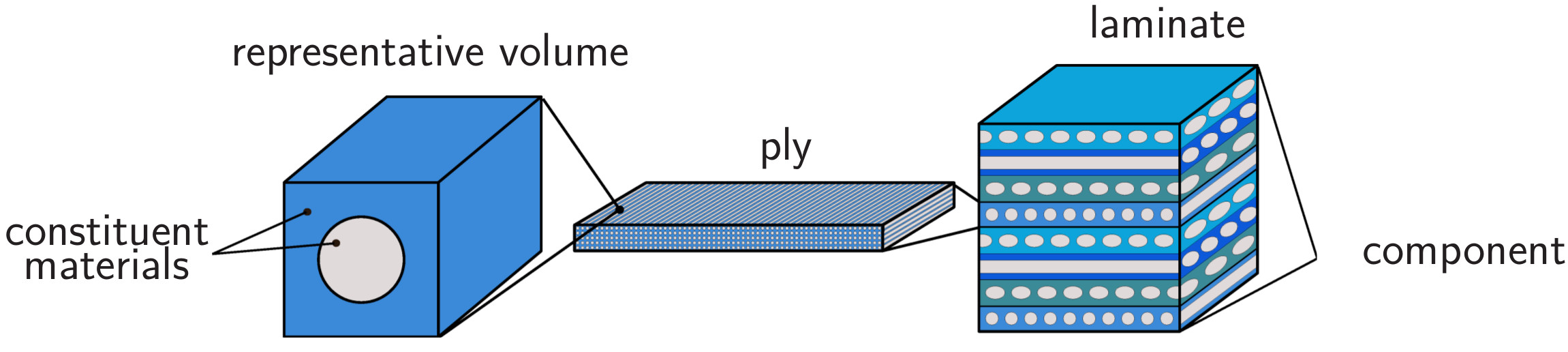
Macroscale – laminate and component

• Natural frequencies, failure strength, buckling strength, fatigue life, interlaminar strength, and residual strength.
• Tools available (PICAN,IPACS) for stochastic analysis based on ply level randomness.

Mesoscale – ply and representative volume element

• Uncertainty from fiber orientation, ply thickness, fiber length and volume ratio, fiber distribution, void volume ratio, inclusions, and debonding.
• Analytical methods (such as Tsai-Wu, Tsai-Hill, Mori-Tanaka) and numerical methods (computational homogenization) are used to characterize ply and RVE response.

Microscale – constituent materials

• Uncertainty at microscale arises from randomness of the materials that make up the composite (fiber and matrix).
• We characterize microscale uncertainty using nonparametric distributions of the parameters that govern the constituent response calibrated from experimental results.

Experiments

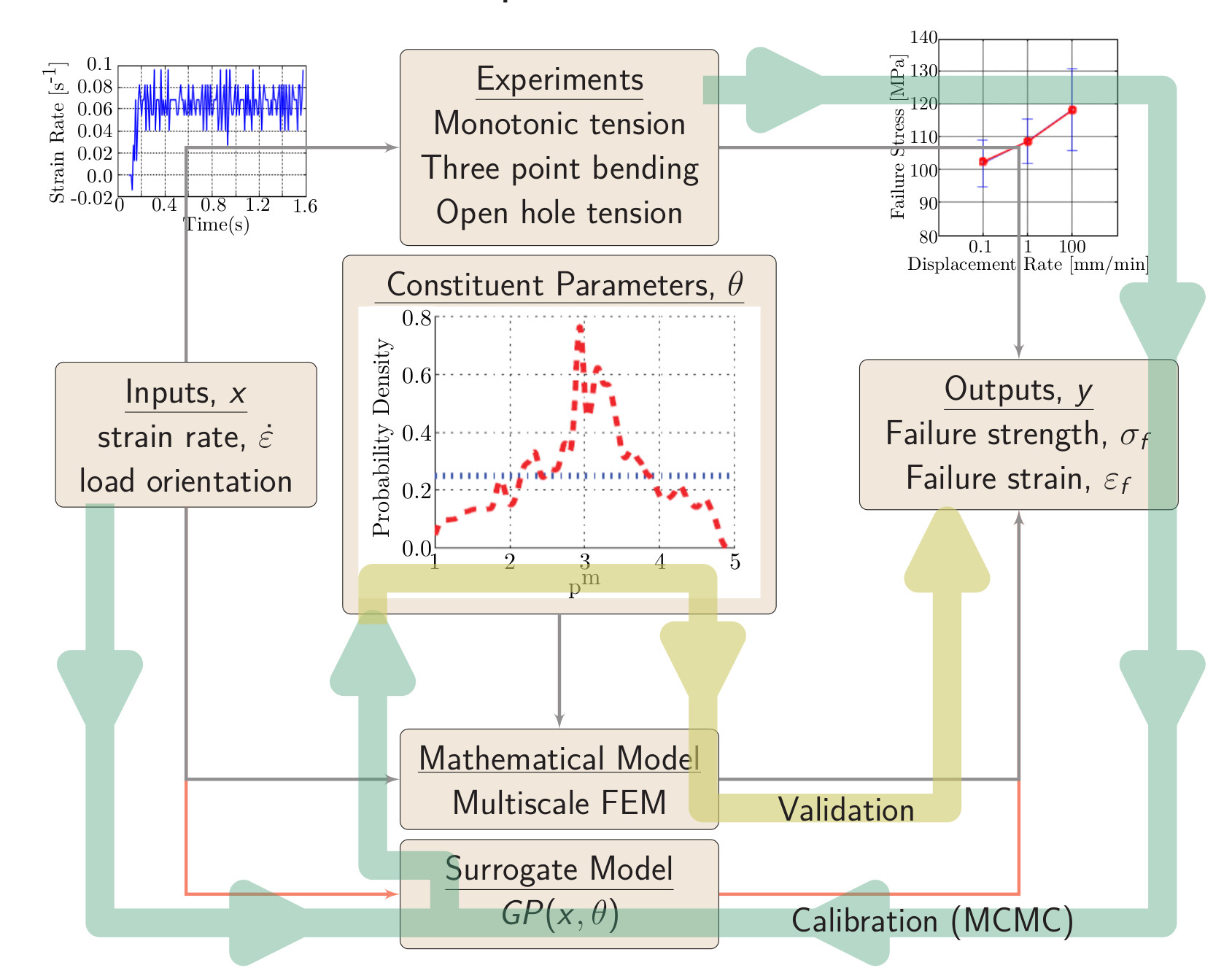
A suite of experiments were conducted at the Air Force Research Laboratory. These experiments were designed to calibrate the random constituent material parameters for the fiber and matrix in IM7/977-3 fiber reinforced polymers and verify the calibrated simulation model against a more complex structure.

Multiscale mechanical model

Eigendeformation based reduced order homogenization

• Computational homogenization analyzes the physical response of the microstructure (RVE) and incorporates this information at the macroscale.
• RVE is partitioned into parts in which stress and damage evolution are uniform throughout the part.
• Influence and homogenization information is precomputed to speed up microscale analysis.
• Continuum Damage Mechanics is employed to track damage and damage induced hardening as an internal state variable in the constituent materials of the composite.

Bayesian Stochastic Parameter Calibration

Bayesian analysis is a means of using conditional probabilities to investigate the relationships between events. Bayesian parameter updating estimates posterior distributions of model parameters based on observed results.

Markov chain Monte Carlo simulation with Metropolis Hastings sampling (MCMC)

• Accelerated sampling technique for calibration.
• Likelihood of parmameters calculated based on agreement with experimental results.

Gaussian Process (GP) surrogate models

• Replace expensive models with accurate predictions which require significantly less computational effort.
• Captures nonlinear response and also is able to identify where the model makes weak or strong predictions.

Ongoing Work

• Investigate spatial variability in material parameters and the length scale effects.
• Implement mechanical models which incorporate macroscopic discontinuities, such as the extended finite element model.
• Calibrate and include in the uncertainty model additional sources of uncertainty at higher scales (i.e. manufacturing error in the RVE and laminate).