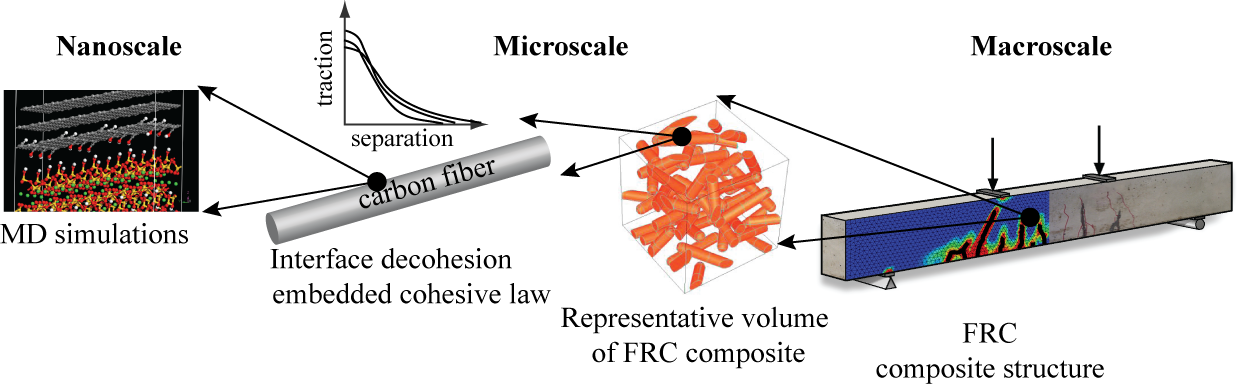
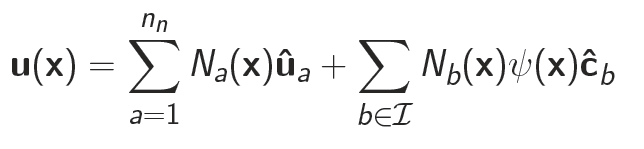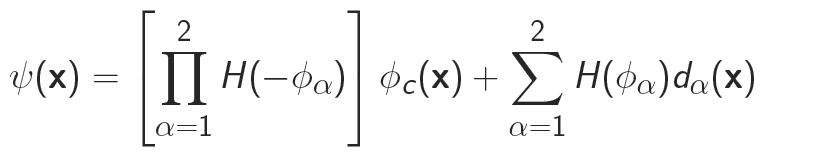Multiscale Modeling of Random Nano- and Micro-Fiber Reinforced Cementitious Composites

Research Sponsor:

Vanderbilt University Grant Research Program

Vanderbilt University Institute for Software Integrated Systems (ISIS)

Investigators:

Matthew G. Pike and Caglar Oskay

Research Goals and Methods

Goals:

To gain a fundamental understanding of the interactions between the fibers and the cement matrix in carbon nano- and micro-fiber reinforced cement composites

To evaluate the effects of the chemical structure of the interface on the macroscopic mechanical failure properties

Multiscale Computational Framework:

Composite response controlled at the molecular scale through the chemical and mechanical interactions

Nanoscale investigations and nanoscopically informed embedded cohesive law

Link the material microstructure to the composite mesoscale: based on the overall response of the RVE

Computational Design of Carbon Nano- and Micro-Fiber Reinforced Cementitious Composites:

Random short fiber reinforced composite material

The inter-facial interaction between the matrix and the reinforcement has significant effect on the overall response of the composite structure

Use of the extended finite element method (X-FEM)to model the fibers in the matrix

Modeling Short Fibers Reinforced Composites Using XFEM

Representative Volume Element (RVE):

Constitutive response of the cohesive zone model for interdependent damage-plasticity modeling of the cement phase

Random short-fiber reinforced matrix idealization

XFEM framework to evaluate the response of the RVE

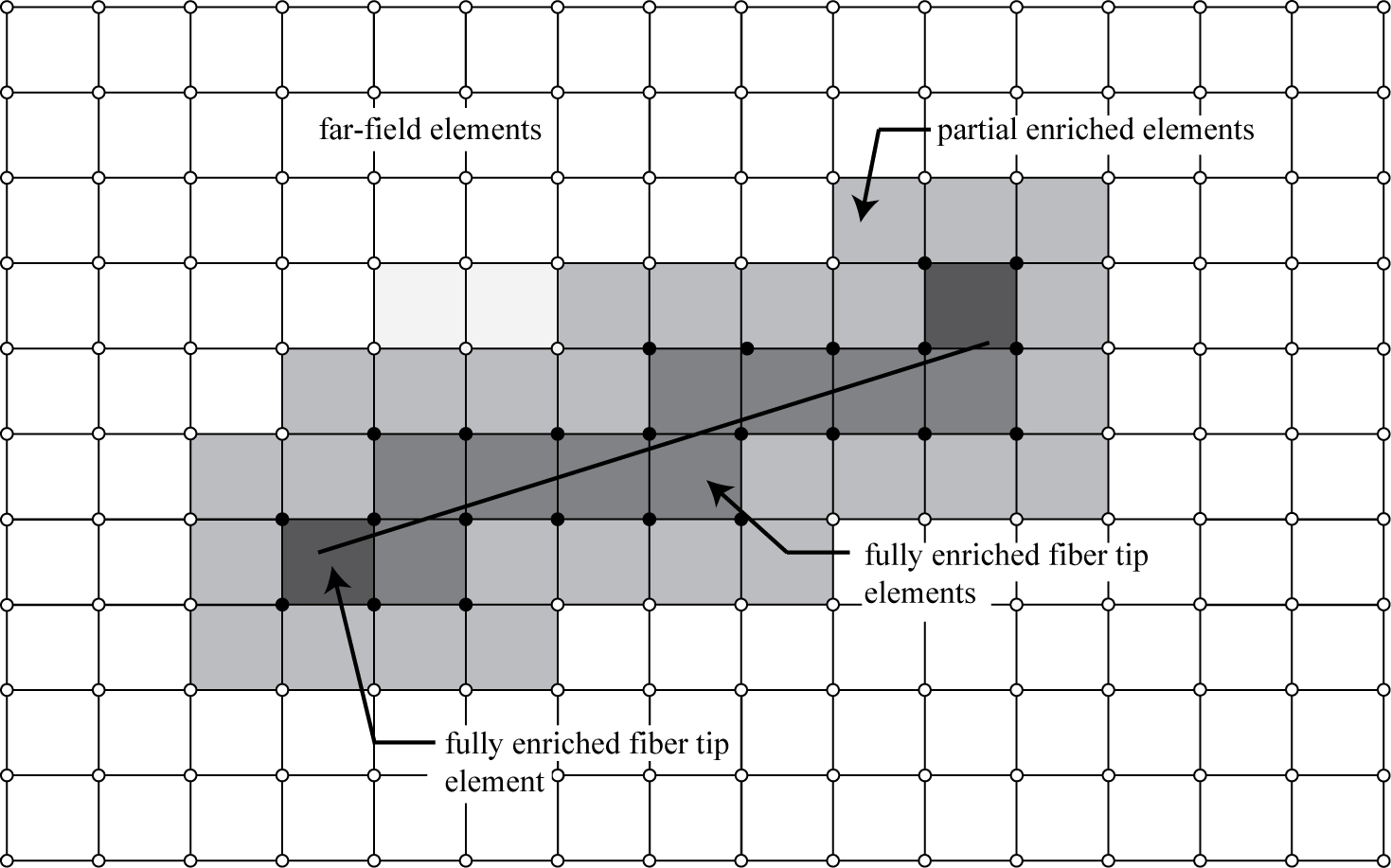
Extended Finite Element Method (XFEM):

Fibers accounted for by using additional enrichment functions

Enrichment of the finite element approximation by additional functions that model the internal boundaries

Fibers can be modeled as rigid or flexible

Complex finite element discretizations that require resolution of fibers are eliminated

N(x): nodal enrichment function, û: nodal value, ψ(x): enrichment function, ĉ: additional degree of freedom nodal value

XFEM Element Types

Nodal Enrichment Function:

Enrichment function of fiber inclusion comprised of level set functions

Level set functions for fiber interface and fiber tips separately

Φ_α(x)=(x–x_i)·t : level set function at fiber tip, i – tracks the motion of each fiber tip

Φ_c(x)=min ||x–x_r|| : level set function at interface – tracks the motion of the fiber interface

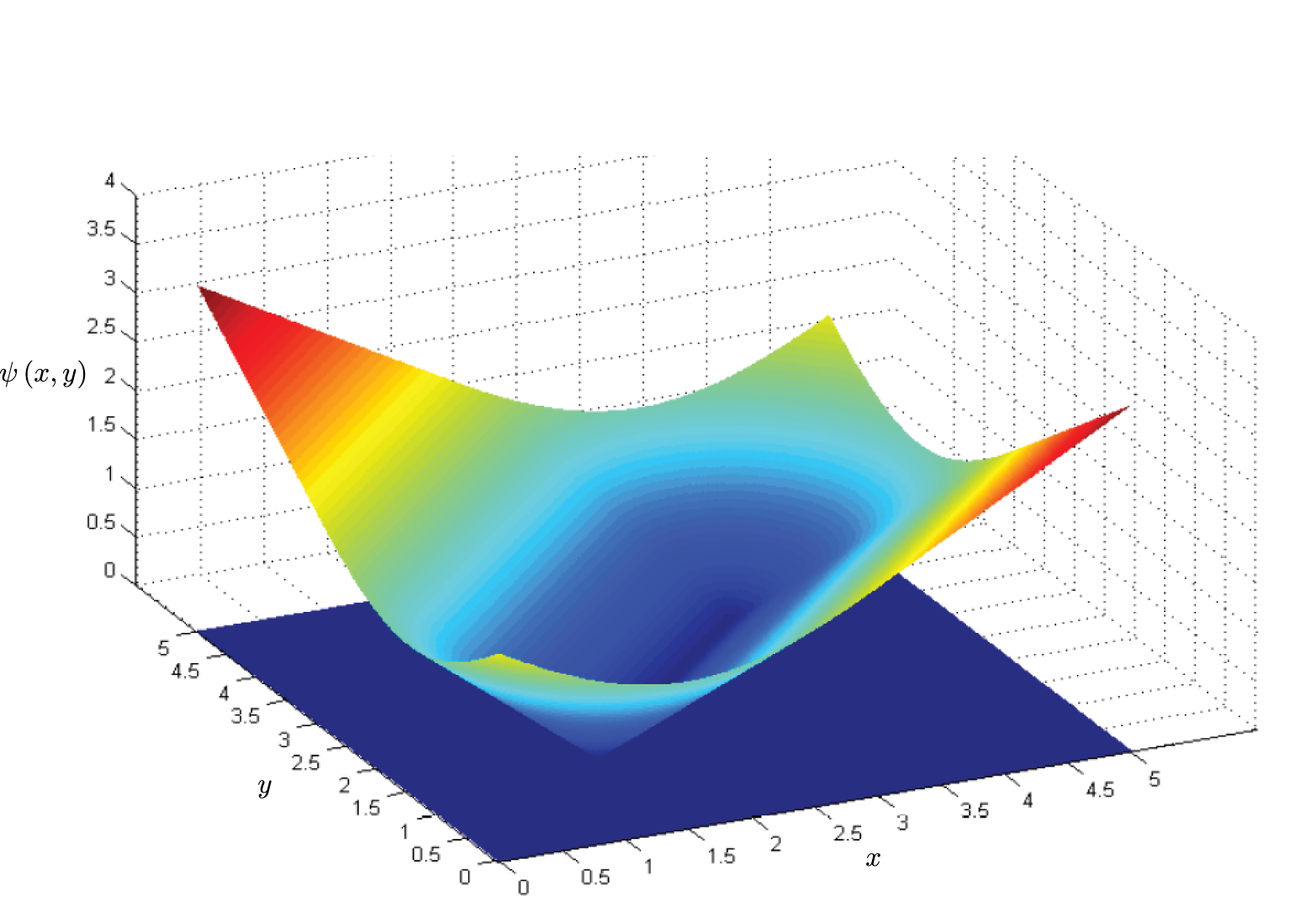Enrichment Function

Enriched Nodal Basis Functions

Fiber Response

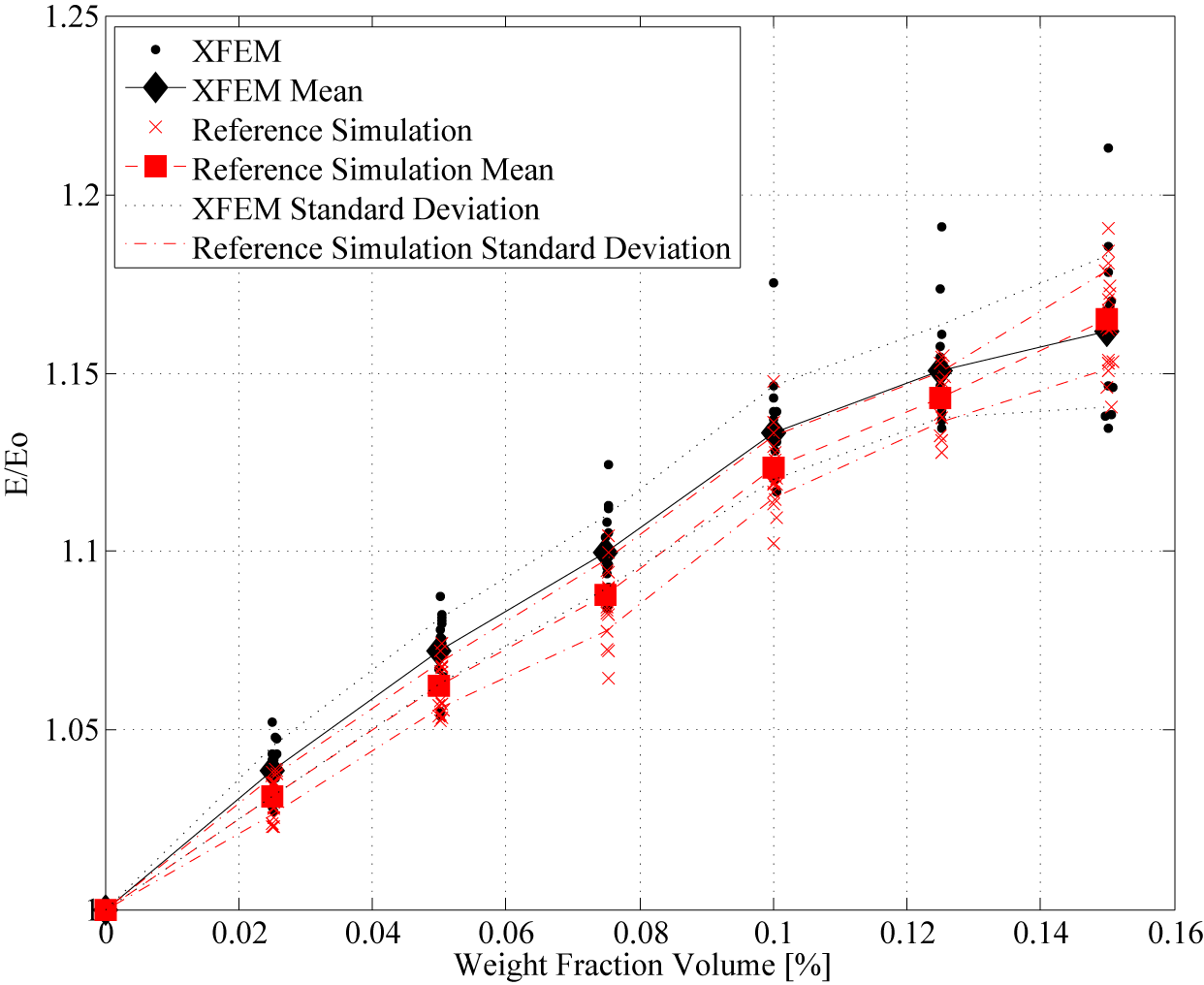
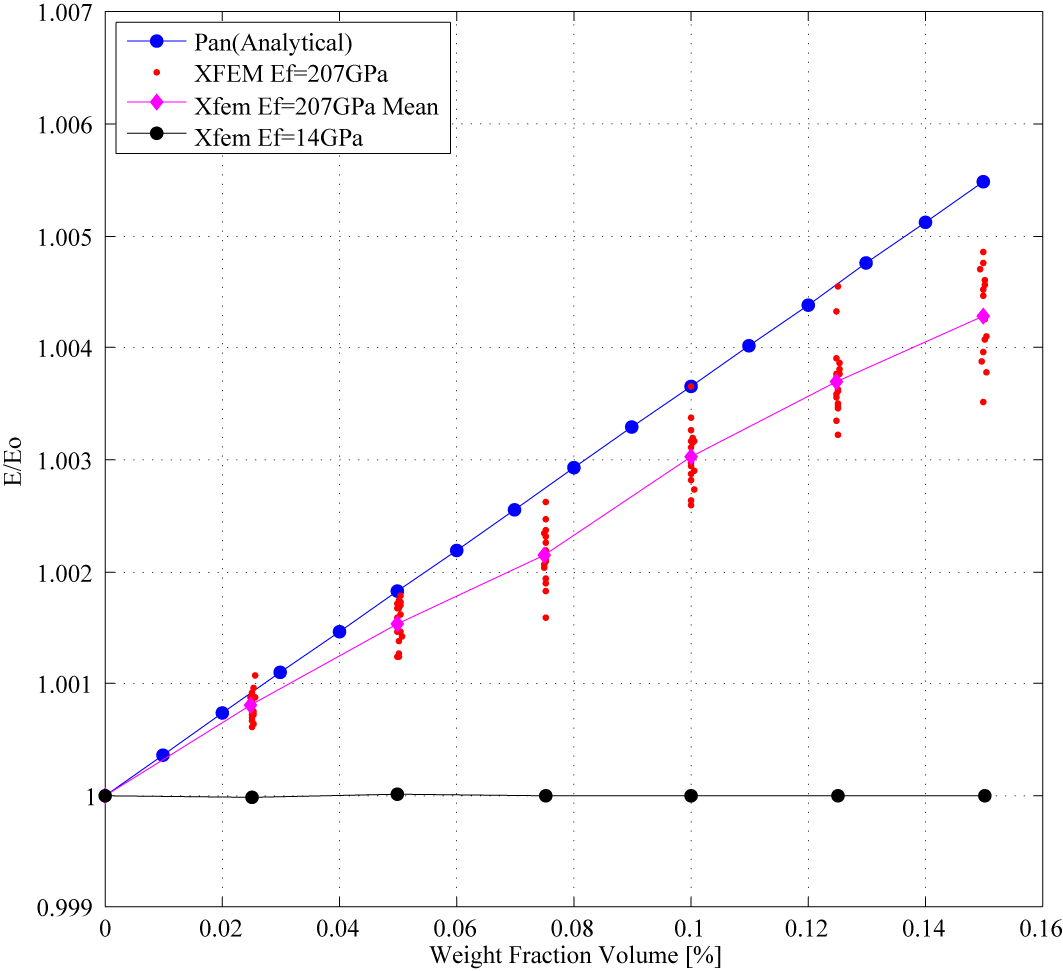
Rigid Fibers:

Assume each fiber moves as a rigid body as does not deform

Described through rotation and translation

Penalty method applied to fiber constraint at fiber/matrix interface

Flexible Fibers:

Assume each fiber is flexible and do not bend but stretch under loading

Flexibility of fiber decrease the strength of the matrix

The energy from the stretch is added to the system

Fiber De-Bonding and Cohesive Embedded Laws

Fiber De-Bonding:

Fibers will de-bond from the matrix once the loading reaches a critical stress

Additional term added to discretization at account for the de-bonding:

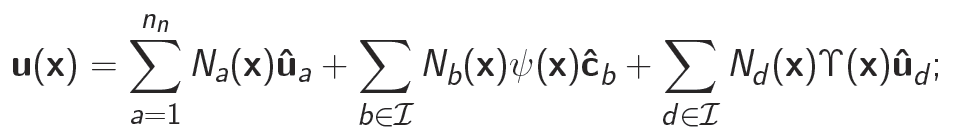
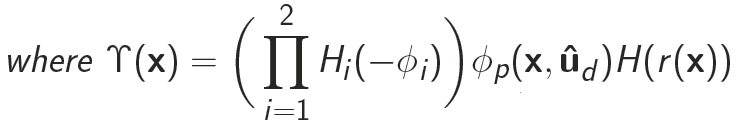
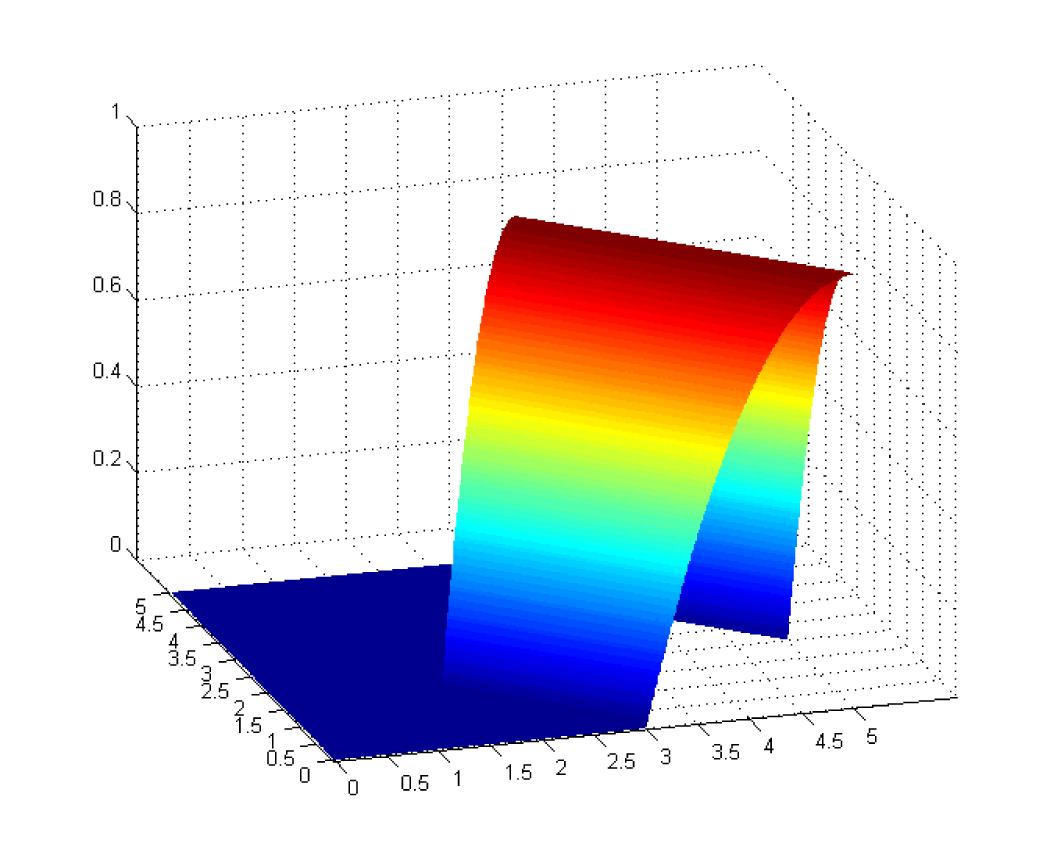De-Bonding Enrichment Function

Cohesive Embedded Law:

Energy based, nanoscopically informed cohesive embedded law

Separation over the interface of the fiber and matrix, resisted by cohesive tractions

Non linear constitutive relationship between cohesive tractions and the displacement jumps along the fiber cement interface as a function of the molecular structure

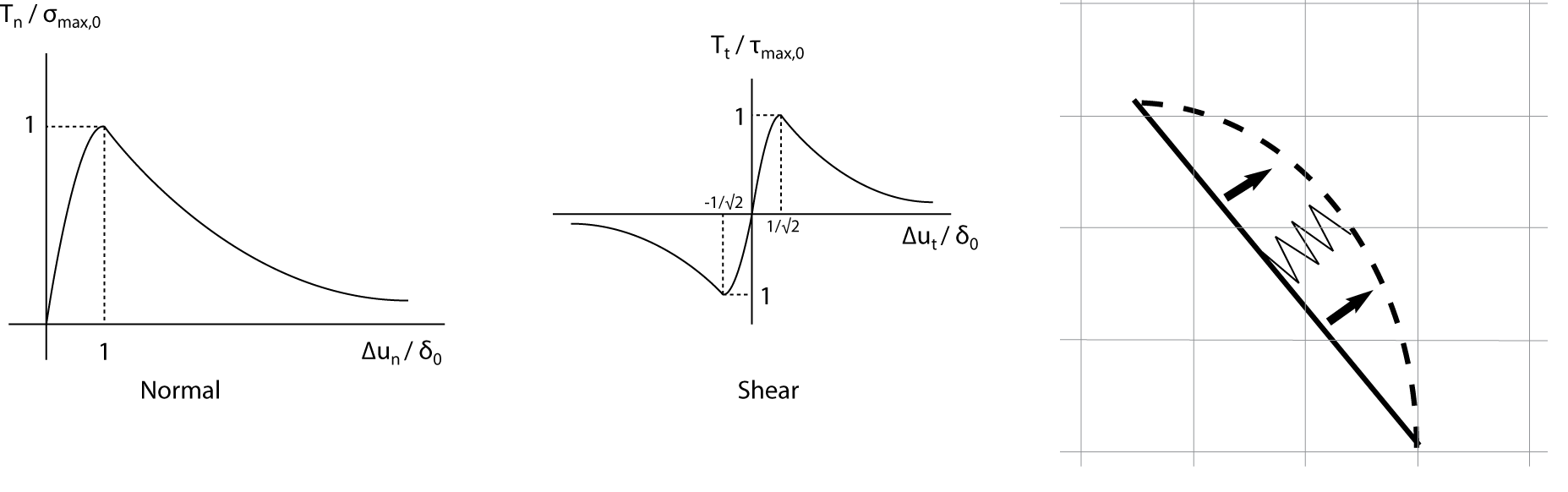Cohesive Traction relationship and Fiber De-Bonding Motion

Summary

Multiscale Computational Framework for Modeling the Mechanical Response of Nano- and Micro-Fiber Reinforced Cementitious Composites:

An efficient XFEM approach is proposed to evaluate the RVE response

Nano- and micro-fibers modeled for rigid, flexibility and de-bonding of fibers

Nanoscale response with the nanoscopically informed cohesive embedded law

Future Potential:

Pathway to achieve simulation based molecular scale engineering of cementitious composites

Aid in the composite material design process