Skip to main content

Multiscale Computational Mechanics Laboratory

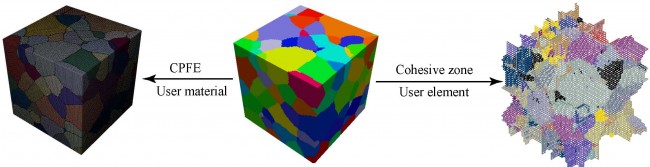
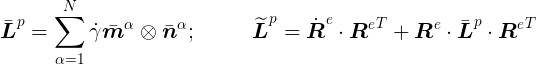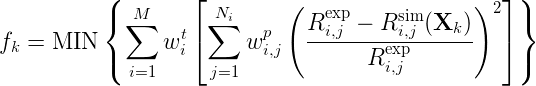Crystal Plasticity Finite Element Modeling of Fatigue and Creep-Fatigue of Alloy 617 at High Temperature

Research Sponsor:

U.S. Department of Energy (DoE), Nuclear Energy University Programs (NEUP) initiative.

Research Goal and Objectives

Goal:

Develop novel testing and experimentally validated prediction methodologies for creep-dominated creep fatigue response of Alloy 617.

Specific Objectives:

  • Formulate and implement models for the simulation of creep fatigue damage mechanisms and their interactions at the microstructure scale.
  • Conduct microstructure simulations to arrive at a better understanding of creep fatigue mechanism while developing a microstructure-informed and experimentally validated phenomenological life prediction framework.

    • Overview of Computational Tasks:

  • Formulation and implementation of a microstructure-based creep fatigue model.
    • Develop CPFE model for Alloy 617 for modeling creep-fatigue deformation between 850°C and 950°C.
    • Simulation-based mechanism understanding of CF interaction and life prediction through exercising the microstructure-based CF model.

  • Simulation-based mechanism understanding of CF interaction and life prediction through exercising the microstructure-based CF model.

    Modeling Approach

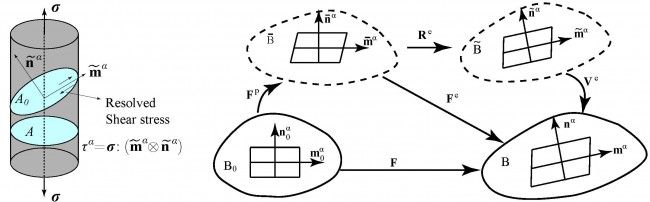
    Crystal Plasticity Theory:

  • Crystallographic slip driven by resolved shear stress are more favored than twin induced deformation for FCC metals.
  • Consider small elastic strain, arbitrary rotations and inelastic strains: applicable for most metals..

    • Formulation

  • Multiplicative decomposition of deformation gradient to and two intermediate configurations:


  • Velocity gradient in different configurations:

  • Decomposition of velocity gradients in different configurations:

    • Choice of Flow Rule and Evolution Equations:

  • Solute drag creep phenomenon.
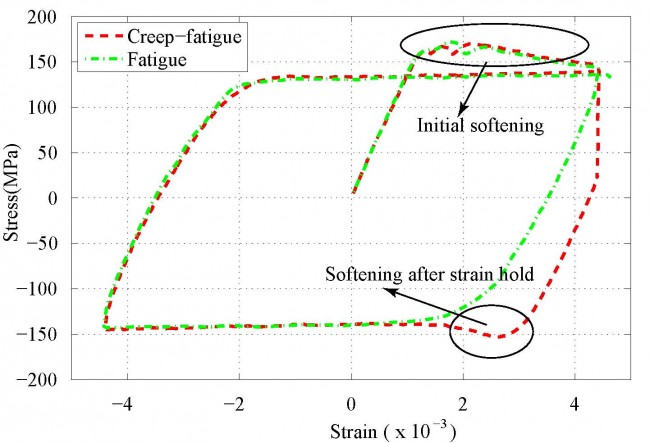
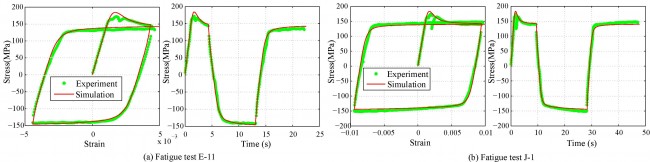
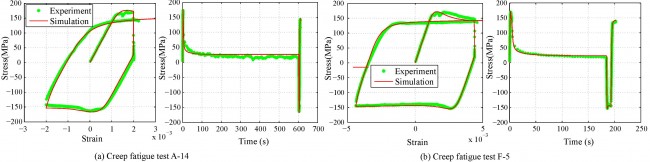
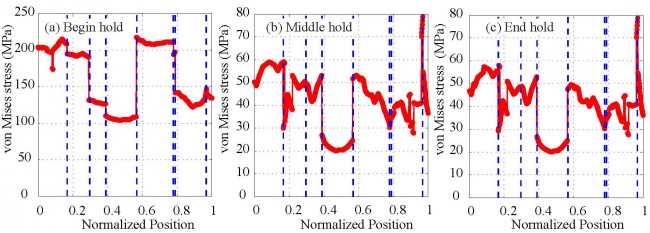
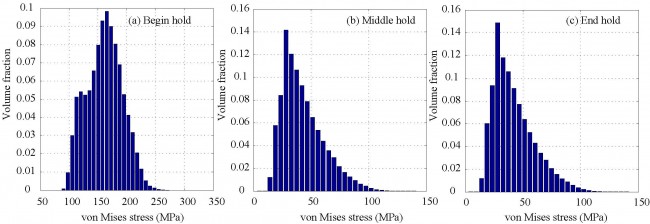
    • Softening is observed at the tension part of first load cycle for both fatigue and creep-fatigue tests. Similar softening is also observed in the compression part after strain hold in each cycle of creep-fatigue tests.

    • Dislocation velocity increases with stress –> dislocation drag solutes hence extra resistance is produced –> dislocations accumulate enough energy to break solutes away from their equilibrium positions –> resistance drops as more and more solutes start moving together with dislocations.
    • Strain hold –> dislocation velocity decreases with stress –> solutes settle down in new equilibrium positions –> softening happens when reverse loading is applied.
    • In a fatigue tests, solutes do not have enough time to settle down in their new equilibrium positions as reverse loading follows immediately.
  • Flow rule and evolution equations to capture solute drag creep.
    • Activation energy based flow rule for nickel-based alloy subject to cyclic loading at high temperatures (Busso[1996]):

    • Slip resistance evolution (Busso[2000]): from statistically stored forest obstacles.

    • Backstress evolution (Busso[1996]): from dislocations bowing between obstacles.

    • New slip resistance evolution equation proposed by incorporating an static recovery which reflects the slip resistance changes caused by solute drag creep.

    • Modeling Preparation and Calibration

    Microstructure reconstruction and meshing

  • Random initial orientation and bi-model grain size distribution from EBSD.

  • Synthetic microstructure reconstruction in DREAM.3D.
  • Surface mesh to volume mesh.

    • Mesh convergence study

  • Stress-strain and stress-time responses converge as grain size increases while computational costs increases.

  • The 140-grain RVE is chosen for all simulations.

    • Model parameter calibration

  • A three stage (elastic, monotonic and hysteresis) calibration process is used to separately calibrate subsets of parameters.
  • A constrained nonlinear constrained optimization process minimizes the objective function:

  • A surrogate model based on Gaussian process to approximate the response during the second and third stages for efficiency.

    • Model Verification and Results Analysis

    Stress-strain and stress-time response simulation.

  • Fatigue tests comparison:

  • Creep fatigue tests comparison:

    • Analysis of CPFE Simulation Results.

  • Stress contour at different stages of the hold of the first cycle:

  • Stress distribution along a line passing the center of the RVE along X direction:

  • Histogram of von Mises stress at different stages of the first cycle:

    • Conclusion and Future Work

    Conclusion

  • Current CPFE model takes the solute drag creep effect into account and well predicts the first cycle responses of fatigue and creep-fatigue tests with different strain range and hold time; It also provides a qualitatively prediction of the cyclic softening.

    • Future Work

  • Cohesive modeling of grain boundaries is ongoing and life prediction capability is expected ultimately.