Accounting for Random Regressors: A Unified Approach to Multi-modality Imaging
Xue Yang, Carolyn B. Lauzon, Ciprian Crainiceanu, Brian Caffo, Susan M. Resnick, Bennett A. Landman. “Accounting for Random Regressors: A Unified Approach to Multi-modality Imaging”, In MICCAI 2011 Workshop of Multi-Modal Brain Image Analysis. Toronto, Canada, September 2011 (Oral Presentation) NIHMS317653 *** BEST PAPER AWARD ***
Full text: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4208720/
Abstract
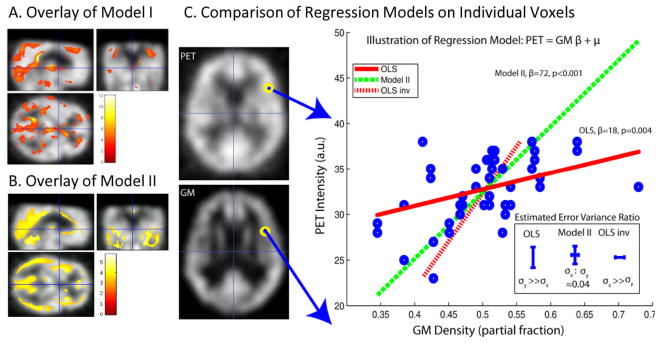
Massively univariate regression and inference in the form of statistical parametric mapping have transformed the way in which multi-dimensional imaging data are studied. In functional and structural neuroimaging, the de facto standard “design matrix”-based general linear regression model and its multi-level cousins have enabled investigation of the biological basis of the human brain. With modern study designs, it is possible to acquire multiple three-dimensional assessments of the same individuals — e.g., structural, functional and quantitative magnetic resonance imaging alongside functional and ligand binding maps with positron emission tomography. Current statistical methods assume that the regressors are non-random. For more realistic multi-parametric assessment (e.g., voxel-wise modeling), distributional consideration of all observations is appropriate (e.g., Model II regression). Herein, we describe a unified regression and inference approach using the design matrix paradigm which accounts for both random and non-random imaging regressors.