Time-Distanced Gates in Long Short-Term Memory Networks
Gao, R., Tang, Y., Xu, K., Huo, Y., Bao, S., Antic, S.L., Epstein, E.S., Deppen, S., Paulson, A.B., Sandler, K.L. and Massion, P.P., Landman, B. A., Time-distanced gates in long short-term memory networks. Medical Image Analysis, 2020.
Full Text: https://pubmed.ncbi.nlm.nih.gov/32745977/
Abstract
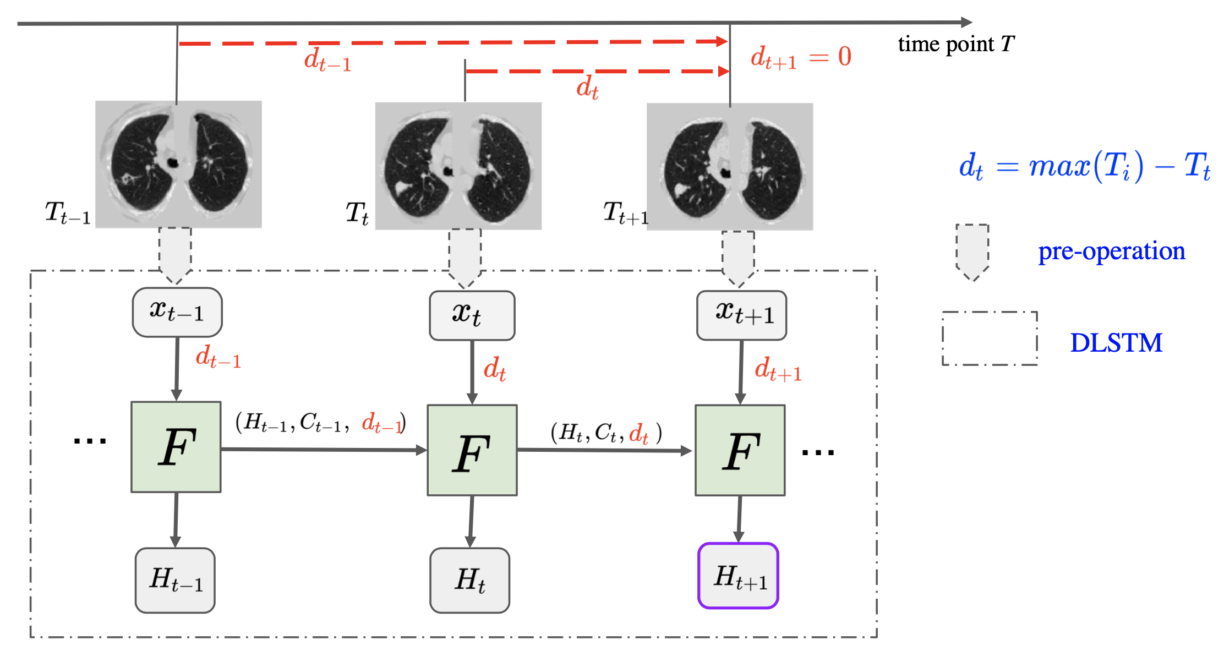
The Long Short-Term Memory (LSTM) network is widely used in modeling sequential observations in fields ranging from natural language processing to medical imaging. The LSTM has shown promise for interpreting computed tomography (CT) in lung screening protocols. Yet, traditional image-based LSTM models ignore interval differences, while recently proposed interval-modeled LSTM variants are limited in their ability to interpret temporal proximity. Meanwhile, clinical imaging acquisition may be irregularly sampled, and such sampling patterns may be commingled with clinical usages. In this paper, we propose the Distanced LSTM (DLSTM) by introducing time-distanced (i.e., time distance to the last scan) gates with a temporal emphasis model (TEM) targeting at lung cancer diagnosis (i.e., evaluating the malignancy of pulmonary nodules). Briefly, (1) the time distance of every scan to the last scan is modeled explicitly, (2) time-distanced input and forget gates in DLSTM are introduced across regular and irregular sampling sequences, and (3) the newer scan in serial data is emphasized by the TEM. The DLSTM algorithm is evaluated with both simulated data and real CT images (from 1794 National Lung Screening Trial (NLST) patients with longitudinal scans and 1420 clinical studied patients). Experimental results on simulated data indicate the DLSTM can capture families of temporal relationships that cannot be detected with traditional LSTM. Cross-validation on empirical CT datasets demonstrates that DLSTM achieves leading performance on both regularly and irregularly sampled data (e.g., improving LSTM from 0.6785 to 0.7085 on F1 score in NLST). In external-validation on irregularly acquired data, the benchmarks achieved 0.8350 (CNN feature) and 0.8380 (with LSTM) on AUC score, while the proposed DLSTM achieves 0.8905. In conclusion, the DLSTM approach is shown to be compatible with families of linear, quadratic, exponential, and log-exponential temporal models. The DLSTM can be readily extended with other temporal dependence interactions while hardly increasing overall model complexity.